Anfang: MO 07 November 2011
Hier nun in chronologischer Reihenfolge alle Themen dieser Startseite; "Unterseiten" gibt es auf dieser Seite auch; sie sind links unter den Linkverbindungen zu sehen; haben aber nur indirekt etwas mit dem Thema zu tun.....
Kapitelübersicht:
1.0) Übersicht
1.1) Einführung
1.2) Beweisidee der fermatschen Vermutung (Fall 1)
1.3) Über Wieferich und Mirimanoff - Primzahlen
Ende: FR 02 März 2012
Montag, 21. November 2011
1.1) Einführung
Anfang: SA 24. April 2010
Auf dieser Unterseite ("Einführung") geht es um die Geschichte (bzw. die historische Entwicklung) des Beweises der fermatschen Vermutung, angefangen von Fermat (Frankreich) selber (welcher diese Vermutung aufgestellt hat) bis hin zu Andrew Wiles (England), der diese Vermutung 1995 beweisen konnte..............
Einer der Folgetexte ("Beweisideen zur fermatschen Vermutung") zeigt dann eine Beweisideen von mir, mit der ich den "Fall 1" der fermatschen Vermutung zu beweisen versucht habe; geelungen ist es mir zwar nicht, aber, ich denke, ich habe zumindest einige neuen Ideen ins Spiel gebracht!
Ausserdem gibt es am Ende noch eine Abhandlung über Wieferich und Mirimannoff-Primzahlen, Primzahlen p also, für die gilt:
(p^2) | 2^(p-1) - 1 (Wieferich-Primzahl)
(p^2) | 3^(p-1) - 1 (Mirimanoff-Primzahl)
Der Begriff "Mirimanoff-Primzahl" ist eine eigene Wortkreation von mir selber; links am Bildrand oben gibt es auch noch einen interessanten Link zu "Wieferich - Primzahlen".
Zu den anderen Links dieser Seite (die man links am Bildschirm anklicken kann, und die sich dann öffnen):
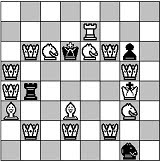
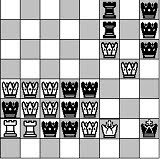
Diese haben (genauso, wie die Schachdiagramme links und die von mir erstellten Artworks darunter) mit Mathematik eigentlich nichts zu tun; eine Erklärung hierfür gibt es links über den Bildern auf einer Unterseite dieser Page ("über diese Seite hier").
Ausserdem gibt es drei Links zu anderen Seiten von mir, der eine davon beschäftigt sich mit "Schachmathematik" (Mathematik im Bezug auf das Schachspiel) bzw. dem "Schach 960" (einer Schachvariante), was nur indirekt etwas mit Mathematik zu tun hat, eine andere Seite widmet sich der Musik, hier sind Eigenkompositionen auf der Gitarre von mir zu finden, die dritte Seite gilt der Philosophie, hier wird die von mir entwickelte philosophische Denkrichtung "Nedilogie" vorgestellt!
Es sei noch erwähnt, dass der beschreibbare Platz nicht größer werden würde, wenn man auf die Bilder links verzichten würde; er wird automatisch freigehalten, so dass hier einige künstlerischen Randnotizen ganz anderer Art stattfinden konnten; die Artworks habe ich am Computer mittels einfacher Bildbearbeitungsprogramme ("Paint" oder aber "Paintbrush") auf der Basis bekannter Bilder (Dali, Maigritte, Tanguy, Helnwein, Ernst, Marc, ect.) erstellt; für mich ist Mathematik halt auch eine Art "Kunst".!
------------------------------------
------------------------------------
------------------------------------
Hier aber nun zum "eigentlichen Thema", der Geschichte der "fermatschen Vermutung" (auch "großer fermatscher Satz" genannt):
------------------------------------------------
Im Jahre 1606, 1607 oder 1608 (fälschlicherweise wird oftmals das Jahr 1901 angegeben) wurde der französische Jurist und (Amateur -) Mathematiker Pierre de Fermat geboren; Richter war sein Hauptberuf, aber, die Mathematik war sein "Hobby", und, da er dort aber sehr begabt war, wurde er oft als "König der Amateure" bezeichnet.
Nach ihm ist z.B. der "kleine fermatsche Satz" benannt; er besagt, dass, sei p eine Primzahl, und, n eine zu dieser Primzahl teilerfremde natürliche Zahl, der Ausdruck
n^(p-1) - 1
immer durch p teilbar sein muss, mathematisch ausgedrückt:
p | n^(p-1) - 1
Wie sein Landsmann und Zeitgenosse Descartes studierte er Rechtswissenschaft. Die beiden haben sogar teilweise die gleichen Entdeckungen gemacht. Fermat soll zum Beispiel schon vor Descartes das Koordinatensystem benutzt haben (Descartes war Universalgelehrter, bekannt aber hauptsächlich als Philosoph mit dem Ausspruch: "Ich denke, also bin ich", auch als "cartesianischer Zweifel" bekannt).
Fermat behauptete irgendwann, dass er beweisen könne, dass, sind x;y und z natürliche Zahlen, und, sei n eine natürliche Zahl, es für den Ausdruck
x^n + y^n = z^n
keine Lösungen gäbe, wenn n ein Exponent sei, der größer als 2 ist. Für den Exponenten 1 gibt es für jedes beliebige Zahlenpaar (x;y) eine Lösung, da gilt:
x^1 + y^1 = z ^1 ist gleich: x + y = z
Für den Exponenten (n = 2) gibt es jedoch nur einige Zahlenpaare (x;y), für die es ganzzahlige (diophantische) Lösungen gibt:
x^2 + y^2 = z^2; die sogenannten "pythagoräischen Zahlentrippel", die schon den griechischen Mathematikern über tausend Jahre zuvor bekannt waren; eines dieser Zahlentrippel ist z.B:
3^2 + 4^2 = 5^2.
Man konnte auch beweisen, dass es unendlich viele dieser Zahlentrippel gibt, da sich jede ungerade Zahl als Differenz zweier aufeinanderfolgender Quadrate darstellen lässt.
Fermat selber konnte seine These für (n = 4) beweisen, und, daraufhin war klar, dass diese in Folge auch als "fermatsche Vermutung" benannte These von ihm nur für ungerade prime Exponenten p und zueinander teilerfremde Basen x,y und z bewiesen zu werden braucht, also, nur für den Ausdruck:
x^p + y^p = z^p,
der Beweis hierfür ist einfach zu finden und wird deswegen von mir hier auch nicht weiter erörtert.....
Fermat schrieb an den Rand eines Buches, er habe einen wahrhaft wunderbaren Beweis dafür gefunden, leider aber sei der Blattrand des Buches zu schmal, um diesen fassen zu können. Sein Sohn, Samuel de Fermat, hat nach dem Tod des Vaters die zahlreichen Briefe und Manuskripte gesammelt und veröffentlicht. Bei dieser Beschäftigung fand er in dem damals wieder entdeckten Werk “Arithmetik” des griechischen Mathematikers Diophant u. a. folgende Randbemerkung:
“Es ist unmöglich, einen Kubus in zwei Kuben zu teilen oder ein Biquadrat in zwei Biquadrate oder irgendeine Potenz in zwei Potenzen gleichen Grades: Ich habe hierfür einen wahrhaft wunderbaren Beweis entdeckt, aber der Rand ist zu klein, ihn zu fassen.”
Seit dieser Zeit gind die "fermatsche Vermutung" (auch als "großer fermatscher Satz" bekannt) in die Geschichte der schwierigsten mathematischen Probleme der Zahlentheorie ein. Weil die Aufgabenstellung so einfach ist, haben sich ganze Heerscharen von Laienmathematikern - so genannte Fermatisten - und große Mathematiker, beispielsweise Leonhard Euler (1707-1783), Eduard Kummer (1810-1893), Friedrich Gauß (1777-1855), mit der Lösung dieses Problems beschäftigt.
Euler konnte zeigen, dass die Gleichung a^3 + b^3 = c^3 im Bereich der natürlichen Zahlen keine Lösung besitzt, wobei er ähnliche Methoden wie Fermat für (n = 4) anwandte, aber, dazu imaginäre Zahlen verwandte. Viele spätere falsche Beweisversuche basieren auf ähnlichen Überlegungen wie die von Euler für p > 3.
Euler selber lebte von 1707 (15. April/ Basel) bis 1783 (18. September St. Petersburg). Er hat so viel geschrieben, wie kein anderer Mathematiker vor oder nach ihm. Seit 1911 werden seine gesammelten Werke herausgegeben.
1742 erhält Euler einen Brief von Goldbach, indem Goldbach eine zahlentheoretische Vermutung aufstellt, die später als sog. "goldbachsche Vermutung" berühmt wird.
Sie besagt, dass jede gerade Zahl n > 2 als Summe zweier Primzahlen darstellbar sein muss; eine bis heute noch unbewiesene Vermutung, welche ebenfalls zu den schwersten Problemen der Zahlentheorie gehört.
Unter den wichtigsten Mathematikern, die sich noch zu Lebzeiten Eulers mit der "fermatschen Vermutung" beschäftigt haben, zählte die deutsche Mathematikerin und Physikerin "Sophie Germain", eine der ganz großen weiblichen Genies in der Mathematik, die die fermatsche Vermutung erstmals für eine ganze Gruppe von primen Exponenten p beweisen konnte, den sogenannten "Sophie-Germain-Primzahlen"; diese Primzahlen p sind Zahlen, für die gilt: (p - 1)/2 ist ebenfalls prim.
Sophie Germain: (* 1. April 1776 in Paris; † 27. Juni 1831 in Paris).
Nach dem Durcharbeiten der Arbeiten der verschiedener Mathematiker schrieb sie eigene Forschungsergebnisse auf und präsentierte diese in einem Briefwechsel Carl Friedrich Gauß ab 1804. Sie tat dies allerdings unter dem Pseudonym Auguste Antoine Le Blanc, weil sie befürchtete, als Frau nicht ernstgenommen zu werden.
Seit 1800 interessiert sie sich für die Zahlentheorie.
Insbesondere arbeitete sie an der Fermatschen Vermutung und bewies um 1805, dass diese Vermutung für alle Sophie-Germain-Primzahlen zutrifft, welche dann später nach ihr benannt worden sind.
In den darauffolgenden Jahren gab es noch weitere bedeutende Beweisversuche von Kummer und Lame.
Im Jahre 1839 zeigte Gabriel Lamé, dass auch der Fall n = 7 Gültigkeit besitzt. Ebenso wie Augustin Louis Cauchy war Lamé noch im März 1847 überzeugt, den vollständigen Beweis für die fermatsche Vermutung innerhalb von Wochen der französischen Akademie der Wissenschaften vorlegen zu können.
Diese Hoffnung wurde aber von Ernst Eduard Kummer zunichte gemacht, der einen Denkfehler in den Überlegungen Lamés und Cauchys entdeckte: Sie waren stillschweigend davon ausgegangen, dass in den von ihnen betrachteten Erweiterungen des Körpers der rationalen Zahlen (Kreisteilungskörpern der Ordnung p) für die jeweilige Fermatgleichung zum Exponent p (er entsteht durch Adjunktion der p-ten Einheitswurzeln) noch die eindeutige Primfaktorzerlegung gilt.
Kummer entwickelte eine Theorie, in der sich die eindeutige Primfaktorzerlegung retten ließ, indem man ganze Gruppen von Zahlen des Zahlkörpers (Ideale) zusammenfasst und die Arithmetik dieser neuen „idealen Zahlen“ untersucht. Er konnte damit den großen fermatschen Satz 1846 für reguläre Primzahlen beweisen.
"Irreguläre Primzahlen" sind Primzahlen mit bestimmten Eigenschaften (diese hier zu beschreiben, wäre zu umständlich); es gibt unendlich viele von diesen (irregulären Primzahlen), aber, weniger als reguläre.
Es tat sich dann lange Zeit sehr wenig, aber, die Mathematik war ein wenig aus ihrem Schattendasein herausgetreten, neue, früher noch unbekannte Methoden wurden entwickelt, und, die "fermatsche Vermutung", eines der schwersten Probleme der Zahlentheorie, entwickelte sich zum "Kultproblem".
Im Jahr 1907 wurde für den Beweis der Wolfskehl-Preis von 100000 Goldmark ausgesetzt für den Beweis der Vermutung.
Gerhard Frey, ein deutscher Mathematiker aus Wuppertal (welcher nicht identisch ist mit dem gleichnamigen rechtsextremen Politiker G.F) zeigte in einem Seminar in dem kleinen Ort "Oberwollfach" (Schwarzwald), (in dem öfters Mathematikseminare abgehalten werden) Ende der 80-er Jahre (war es 1988 ?), dass die fermatsche Vermutung komplett bewiesen werden konnte, wenn die Taniyama-Shimura-Vermutung bewiesen werden könne;
Yutaka Taniyama wuchs in einem kleinen Dorf bei Tokio (Japan) auf. 1953 graduierte er an der Universität Tokio und wurde dort danach Forschungsstudent und Assistenzprofessor. Gemeinsam mit seinem Freund Goro Shimura (beide Japaner lernten sich per Zufall kennen), welcher viele seiner Arbeiten nach seinem Tod fortsetzte, stellte er 1955–1957 die Taniyama-Shimura-Vermutung auf, welche besagt, dass elliptische Kurven über den rationalen Zahlen immer auch als Modulformen ausgedrückt werden können. Die Ausformulierung und die Propagierung der Wichtigkeit dieser Vermutung stammt von André Weil (deshalb wird auch manchmal sein Name an die Vermutung angehängt), der Shimura und Taniyama 1955 auf einer Konferenz über algebraische Zahlentheorie in Tokio begegnete.
Dabei machte G. Fray in dem Seminar jedoch einen Fehler, welcher später dann von dem US - Mathematiker Kenneth Alan Ribet (* 28. Juni 1948) unter Mithilfe seines ehemaligen Dozenten Joan Coates bereinigt werden konnte; angeblich bei einer Tasse Cappuccino in einem Straßencafe. Seitdem war klar: Wer die Taniyama-Shimura-Vermutung beweisen konnte, der konnte auch die fermatsche Vermutung beweisen; dies war der eigentliche Verdienst von Frey.
Im Juni 1993, verbreitete sich die Nachricht:
“Andrew Wiles hat die Fermatsche Vermutung bewiesen”
Tatsächlich stellte sich heraus, dass im Beweis eine riesige Lücke vorhanden war, welche Wiles leider zunächst entgangen war, und, von Richard Taylor entdeckt wurde; Taylor war in erster Linie für die Überprüfung des Beweises zuständig.
Bereits ein Jahr später aber gelang es dem Engländer Wiles mit Hilfe seines Schülers Richard Taylor, diese zu schließen und damit wohl endgültig die berühmteste unter den mathematischen Vermutungen zu beweisen.
Die Schlüsselidee zum Beweis stammt prinzipiell von dem deutschen Mathematiker Gerhard Frey. Mit Hilfe der Iwasawa-Theorie und der Kolywagin-Flach-Methode gelang es Wiles, die Fermatsche Vermutung zu beweisen.
Der Beweis ist ausgesprochen kompliziert, umfasst 170 Seiten und ist wohl nur von sehr wenigen Mathematikern vollständig zu verstehen.
Die darin angewandten Methoden sind derart fortschrittlich, dass auszuschliessen ist, das Fermat den Beweis in dieser Form damals gefunden haben könnte.
Eine wichtige Literatur hierzu ist:
Fermats letzter Satz. dtv, München 2000, ISBN 3-423-33052-X.
Das Buch ist popularwissenschaftlich gehalten, und, weist wohl auch noch einige Fehler und Ungenauigkeiten auf, liest sich aber recht flüssig und bietet den wichtigsten Überblick zum Beweis der fermatschen Vermutung.
Anschliessend noch eine Auflistung von Mathematikern (Évariste Galois; Johann Carl Friedrich Gauß, Gerd Faltings), welche zwar nur indirekt mit der fermatschen Vermutung zu tun haben, aber, nicht unerwähnt bleiben sollen. Ganz am Schluss widme ich mich der "Fields-Medaille".
Évariste Galois (* 25. Oktober 1811 in Bourg-la-Reine; † 31. Mai 1832 in Paris) war ein französischer Mathematiker. Er starb im Alter von nur 20 Jahren bei einem Duell, erlangte allerdings durch seine Arbeiten zur Lösung algebraischer Gleichungen, der so genannten Galoistheorie, postum Anerkennung; er hat allerdeings wenig Schriftliches von seinem Wissen hinterlassen; die Gründe für seinen frühen Tod lagen unter Anderem darin, dass er ein Anhänger der französischen Revolution gewesen sein soll.
Johann Carl Friedrich Gauß (latinisiert Carolus Fridericus Gauss; * 30. April 1777 in Braunschweig; † 23. Februar 1855 in Göttingen) war ein deutscher Mathematiker, Astronom, Geodät und Physiker mit einem breit gefächerten Feld an Interessen.
Gerd Faltings (* 28. Juli 1954 in Gelsenkirchen-Buer + ca 2008 bis 2011) ist ein deutscher Mathematiker und Träger der Fields-Medaille.
Er konnte beweisen, dass, wenn es "fermatsche Lösungstrippel" gab, diese Trippel nur für eine endliche Zahl von Exponenten und Basen gelten konnte.
Nun zur "Fields-Medaille":
Die Fields-Medaille, offizieller Name International Medal for Outstanding Discoveries in Mathematics (deutsch: Internationale Medaille für herausragende Entdeckungen in der Mathematik), ist eine der höchsten Auszeichnungen, die man als Mathematiker erhalten kann.
Die Empfänger der Medaille müssen vor dem 1. Januar des Jahres, in dem sie ausgezeichnet werden, jünger als 40 Jahre gewesen sein.
Dieser Preis gilt als eine Art "Nobelpreis" für Mathematiker; Nobelpreise gibt es nur in den Sparten Physik, Chemie, Medizin, Literatur sowie den "Friedensnobelpreis". Manche sagen, dass Nobel auch für die Mathematik einen solchen Preis einführen wollte, dies jeoch wegen einem Streit mit einem Mathematiker nicht geschah.
Die Klausel mit der Altersgrenze verhinderte zum Beispiel die Verleihung an Andrew Wiles (* 1953), dem der Beweis des Modularitätssatzes (aus dem der große fermatsche Satz folgt) erst 1993 teilweise und 1995 vollständig gelang. Wiles erhielt stattdessen auf dem ICM 1998 in Berlin eine Sonderauszeichnung der IMU, verbunden mit einer Silberplakette.
Ich möchte hervorheben, dass ich selber die wichtigsten Informationen zu diesem Thema nur durch das Internet erhalten habe (welches zum Teil widersprüchliche Angaben lieferte), und, manche Textabschnitte dort heraus einfach nur kopiert habe, allerdings nie Kopien mit allzulangen Texten, weswegen ich hoffe, hier keine urheberrechtlichen Schwierigkeiten zu bekommen.
Für die inhaltliche Richtigkeit des von mir hier Gesagtem kann ich somit also auch nur zum Teil geradestehen, zumal ich kaum die Möglichkeit zu einer "objektiven Recherche" habe; sollten sich also Fehler darin finden, so sind diese von meiner Seite aus unbeabsichtigt; keinesfalls entspricht es jedoch meiner Intention, den Ruf irgendwelcher Personen zu schmälern.
Ende: MI 22 Februar 2012
Auf dieser Unterseite ("Einführung") geht es um die Geschichte (bzw. die historische Entwicklung) des Beweises der fermatschen Vermutung, angefangen von Fermat (Frankreich) selber (welcher diese Vermutung aufgestellt hat) bis hin zu Andrew Wiles (England), der diese Vermutung 1995 beweisen konnte..............
Einer der Folgetexte ("Beweisideen zur fermatschen Vermutung") zeigt dann eine Beweisideen von mir, mit der ich den "Fall 1" der fermatschen Vermutung zu beweisen versucht habe; geelungen ist es mir zwar nicht, aber, ich denke, ich habe zumindest einige neuen Ideen ins Spiel gebracht!
Ausserdem gibt es am Ende noch eine Abhandlung über Wieferich und Mirimannoff-Primzahlen, Primzahlen p also, für die gilt:
(p^2) | 2^(p-1) - 1 (Wieferich-Primzahl)
(p^2) | 3^(p-1) - 1 (Mirimanoff-Primzahl)
Der Begriff "Mirimanoff-Primzahl" ist eine eigene Wortkreation von mir selber; links am Bildrand oben gibt es auch noch einen interessanten Link zu "Wieferich - Primzahlen".
Zu den anderen Links dieser Seite (die man links am Bildschirm anklicken kann, und die sich dann öffnen):
Diese haben (genauso, wie die Schachdiagramme links und die von mir erstellten Artworks darunter) mit Mathematik eigentlich nichts zu tun; eine Erklärung hierfür gibt es links über den Bildern auf einer Unterseite dieser Page ("über diese Seite hier").
Ausserdem gibt es drei Links zu anderen Seiten von mir, der eine davon beschäftigt sich mit "Schachmathematik" (Mathematik im Bezug auf das Schachspiel) bzw. dem "Schach 960" (einer Schachvariante), was nur indirekt etwas mit Mathematik zu tun hat, eine andere Seite widmet sich der Musik, hier sind Eigenkompositionen auf der Gitarre von mir zu finden, die dritte Seite gilt der Philosophie, hier wird die von mir entwickelte philosophische Denkrichtung "Nedilogie" vorgestellt!
Es sei noch erwähnt, dass der beschreibbare Platz nicht größer werden würde, wenn man auf die Bilder links verzichten würde; er wird automatisch freigehalten, so dass hier einige künstlerischen Randnotizen ganz anderer Art stattfinden konnten; die Artworks habe ich am Computer mittels einfacher Bildbearbeitungsprogramme ("Paint" oder aber "Paintbrush") auf der Basis bekannter Bilder (Dali, Maigritte, Tanguy, Helnwein, Ernst, Marc, ect.) erstellt; für mich ist Mathematik halt auch eine Art "Kunst".!
------------------------------------
------------------------------------
------------------------------------
Hier aber nun zum "eigentlichen Thema", der Geschichte der "fermatschen Vermutung" (auch "großer fermatscher Satz" genannt):
------------------------------------------------
Im Jahre 1606, 1607 oder 1608 (fälschlicherweise wird oftmals das Jahr 1901 angegeben) wurde der französische Jurist und (Amateur -) Mathematiker Pierre de Fermat geboren; Richter war sein Hauptberuf, aber, die Mathematik war sein "Hobby", und, da er dort aber sehr begabt war, wurde er oft als "König der Amateure" bezeichnet.
Nach ihm ist z.B. der "kleine fermatsche Satz" benannt; er besagt, dass, sei p eine Primzahl, und, n eine zu dieser Primzahl teilerfremde natürliche Zahl, der Ausdruck
n^(p-1) - 1
immer durch p teilbar sein muss, mathematisch ausgedrückt:
p | n^(p-1) - 1
Wie sein Landsmann und Zeitgenosse Descartes studierte er Rechtswissenschaft. Die beiden haben sogar teilweise die gleichen Entdeckungen gemacht. Fermat soll zum Beispiel schon vor Descartes das Koordinatensystem benutzt haben (Descartes war Universalgelehrter, bekannt aber hauptsächlich als Philosoph mit dem Ausspruch: "Ich denke, also bin ich", auch als "cartesianischer Zweifel" bekannt).
Fermat behauptete irgendwann, dass er beweisen könne, dass, sind x;y und z natürliche Zahlen, und, sei n eine natürliche Zahl, es für den Ausdruck
x^n + y^n = z^n
keine Lösungen gäbe, wenn n ein Exponent sei, der größer als 2 ist. Für den Exponenten 1 gibt es für jedes beliebige Zahlenpaar (x;y) eine Lösung, da gilt:
x^1 + y^1 = z ^1 ist gleich: x + y = z
Für den Exponenten (n = 2) gibt es jedoch nur einige Zahlenpaare (x;y), für die es ganzzahlige (diophantische) Lösungen gibt:
x^2 + y^2 = z^2; die sogenannten "pythagoräischen Zahlentrippel", die schon den griechischen Mathematikern über tausend Jahre zuvor bekannt waren; eines dieser Zahlentrippel ist z.B:
3^2 + 4^2 = 5^2.
Man konnte auch beweisen, dass es unendlich viele dieser Zahlentrippel gibt, da sich jede ungerade Zahl als Differenz zweier aufeinanderfolgender Quadrate darstellen lässt.
Fermat selber konnte seine These für (n = 4) beweisen, und, daraufhin war klar, dass diese in Folge auch als "fermatsche Vermutung" benannte These von ihm nur für ungerade prime Exponenten p und zueinander teilerfremde Basen x,y und z bewiesen zu werden braucht, also, nur für den Ausdruck:
x^p + y^p = z^p,
der Beweis hierfür ist einfach zu finden und wird deswegen von mir hier auch nicht weiter erörtert.....
Fermat schrieb an den Rand eines Buches, er habe einen wahrhaft wunderbaren Beweis dafür gefunden, leider aber sei der Blattrand des Buches zu schmal, um diesen fassen zu können. Sein Sohn, Samuel de Fermat, hat nach dem Tod des Vaters die zahlreichen Briefe und Manuskripte gesammelt und veröffentlicht. Bei dieser Beschäftigung fand er in dem damals wieder entdeckten Werk “Arithmetik” des griechischen Mathematikers Diophant u. a. folgende Randbemerkung:
“Es ist unmöglich, einen Kubus in zwei Kuben zu teilen oder ein Biquadrat in zwei Biquadrate oder irgendeine Potenz in zwei Potenzen gleichen Grades: Ich habe hierfür einen wahrhaft wunderbaren Beweis entdeckt, aber der Rand ist zu klein, ihn zu fassen.”
Seit dieser Zeit gind die "fermatsche Vermutung" (auch als "großer fermatscher Satz" bekannt) in die Geschichte der schwierigsten mathematischen Probleme der Zahlentheorie ein. Weil die Aufgabenstellung so einfach ist, haben sich ganze Heerscharen von Laienmathematikern - so genannte Fermatisten - und große Mathematiker, beispielsweise Leonhard Euler (1707-1783), Eduard Kummer (1810-1893), Friedrich Gauß (1777-1855), mit der Lösung dieses Problems beschäftigt.
Euler konnte zeigen, dass die Gleichung a^3 + b^3 = c^3 im Bereich der natürlichen Zahlen keine Lösung besitzt, wobei er ähnliche Methoden wie Fermat für (n = 4) anwandte, aber, dazu imaginäre Zahlen verwandte. Viele spätere falsche Beweisversuche basieren auf ähnlichen Überlegungen wie die von Euler für p > 3.
Euler selber lebte von 1707 (15. April/ Basel) bis 1783 (18. September St. Petersburg). Er hat so viel geschrieben, wie kein anderer Mathematiker vor oder nach ihm. Seit 1911 werden seine gesammelten Werke herausgegeben.
1742 erhält Euler einen Brief von Goldbach, indem Goldbach eine zahlentheoretische Vermutung aufstellt, die später als sog. "goldbachsche Vermutung" berühmt wird.
Sie besagt, dass jede gerade Zahl n > 2 als Summe zweier Primzahlen darstellbar sein muss; eine bis heute noch unbewiesene Vermutung, welche ebenfalls zu den schwersten Problemen der Zahlentheorie gehört.
Unter den wichtigsten Mathematikern, die sich noch zu Lebzeiten Eulers mit der "fermatschen Vermutung" beschäftigt haben, zählte die deutsche Mathematikerin und Physikerin "Sophie Germain", eine der ganz großen weiblichen Genies in der Mathematik, die die fermatsche Vermutung erstmals für eine ganze Gruppe von primen Exponenten p beweisen konnte, den sogenannten "Sophie-Germain-Primzahlen"; diese Primzahlen p sind Zahlen, für die gilt: (p - 1)/2 ist ebenfalls prim.
Sophie Germain: (* 1. April 1776 in Paris; † 27. Juni 1831 in Paris).
Nach dem Durcharbeiten der Arbeiten der verschiedener Mathematiker schrieb sie eigene Forschungsergebnisse auf und präsentierte diese in einem Briefwechsel Carl Friedrich Gauß ab 1804. Sie tat dies allerdings unter dem Pseudonym Auguste Antoine Le Blanc, weil sie befürchtete, als Frau nicht ernstgenommen zu werden.
Seit 1800 interessiert sie sich für die Zahlentheorie.
Insbesondere arbeitete sie an der Fermatschen Vermutung und bewies um 1805, dass diese Vermutung für alle Sophie-Germain-Primzahlen zutrifft, welche dann später nach ihr benannt worden sind.
In den darauffolgenden Jahren gab es noch weitere bedeutende Beweisversuche von Kummer und Lame.
Im Jahre 1839 zeigte Gabriel Lamé, dass auch der Fall n = 7 Gültigkeit besitzt. Ebenso wie Augustin Louis Cauchy war Lamé noch im März 1847 überzeugt, den vollständigen Beweis für die fermatsche Vermutung innerhalb von Wochen der französischen Akademie der Wissenschaften vorlegen zu können.
Diese Hoffnung wurde aber von Ernst Eduard Kummer zunichte gemacht, der einen Denkfehler in den Überlegungen Lamés und Cauchys entdeckte: Sie waren stillschweigend davon ausgegangen, dass in den von ihnen betrachteten Erweiterungen des Körpers der rationalen Zahlen (Kreisteilungskörpern der Ordnung p) für die jeweilige Fermatgleichung zum Exponent p (er entsteht durch Adjunktion der p-ten Einheitswurzeln) noch die eindeutige Primfaktorzerlegung gilt.
Kummer entwickelte eine Theorie, in der sich die eindeutige Primfaktorzerlegung retten ließ, indem man ganze Gruppen von Zahlen des Zahlkörpers (Ideale) zusammenfasst und die Arithmetik dieser neuen „idealen Zahlen“ untersucht. Er konnte damit den großen fermatschen Satz 1846 für reguläre Primzahlen beweisen.
"Irreguläre Primzahlen" sind Primzahlen mit bestimmten Eigenschaften (diese hier zu beschreiben, wäre zu umständlich); es gibt unendlich viele von diesen (irregulären Primzahlen), aber, weniger als reguläre.
Es tat sich dann lange Zeit sehr wenig, aber, die Mathematik war ein wenig aus ihrem Schattendasein herausgetreten, neue, früher noch unbekannte Methoden wurden entwickelt, und, die "fermatsche Vermutung", eines der schwersten Probleme der Zahlentheorie, entwickelte sich zum "Kultproblem".
Im Jahr 1907 wurde für den Beweis der Wolfskehl-Preis von 100000 Goldmark ausgesetzt für den Beweis der Vermutung.
Gerhard Frey, ein deutscher Mathematiker aus Wuppertal (welcher nicht identisch ist mit dem gleichnamigen rechtsextremen Politiker G.F) zeigte in einem Seminar in dem kleinen Ort "Oberwollfach" (Schwarzwald), (in dem öfters Mathematikseminare abgehalten werden) Ende der 80-er Jahre (war es 1988 ?), dass die fermatsche Vermutung komplett bewiesen werden konnte, wenn die Taniyama-Shimura-Vermutung bewiesen werden könne;
Yutaka Taniyama wuchs in einem kleinen Dorf bei Tokio (Japan) auf. 1953 graduierte er an der Universität Tokio und wurde dort danach Forschungsstudent und Assistenzprofessor. Gemeinsam mit seinem Freund Goro Shimura (beide Japaner lernten sich per Zufall kennen), welcher viele seiner Arbeiten nach seinem Tod fortsetzte, stellte er 1955–1957 die Taniyama-Shimura-Vermutung auf, welche besagt, dass elliptische Kurven über den rationalen Zahlen immer auch als Modulformen ausgedrückt werden können. Die Ausformulierung und die Propagierung der Wichtigkeit dieser Vermutung stammt von André Weil (deshalb wird auch manchmal sein Name an die Vermutung angehängt), der Shimura und Taniyama 1955 auf einer Konferenz über algebraische Zahlentheorie in Tokio begegnete.
Dabei machte G. Fray in dem Seminar jedoch einen Fehler, welcher später dann von dem US - Mathematiker Kenneth Alan Ribet (* 28. Juni 1948) unter Mithilfe seines ehemaligen Dozenten Joan Coates bereinigt werden konnte; angeblich bei einer Tasse Cappuccino in einem Straßencafe. Seitdem war klar: Wer die Taniyama-Shimura-Vermutung beweisen konnte, der konnte auch die fermatsche Vermutung beweisen; dies war der eigentliche Verdienst von Frey.
Im Juni 1993, verbreitete sich die Nachricht:
“Andrew Wiles hat die Fermatsche Vermutung bewiesen”
Tatsächlich stellte sich heraus, dass im Beweis eine riesige Lücke vorhanden war, welche Wiles leider zunächst entgangen war, und, von Richard Taylor entdeckt wurde; Taylor war in erster Linie für die Überprüfung des Beweises zuständig.
Bereits ein Jahr später aber gelang es dem Engländer Wiles mit Hilfe seines Schülers Richard Taylor, diese zu schließen und damit wohl endgültig die berühmteste unter den mathematischen Vermutungen zu beweisen.
Die Schlüsselidee zum Beweis stammt prinzipiell von dem deutschen Mathematiker Gerhard Frey. Mit Hilfe der Iwasawa-Theorie und der Kolywagin-Flach-Methode gelang es Wiles, die Fermatsche Vermutung zu beweisen.
Der Beweis ist ausgesprochen kompliziert, umfasst 170 Seiten und ist wohl nur von sehr wenigen Mathematikern vollständig zu verstehen.
Die darin angewandten Methoden sind derart fortschrittlich, dass auszuschliessen ist, das Fermat den Beweis in dieser Form damals gefunden haben könnte.
Eine wichtige Literatur hierzu ist:
Fermats letzter Satz. dtv, München 2000, ISBN 3-423-33052-X.
Das Buch ist popularwissenschaftlich gehalten, und, weist wohl auch noch einige Fehler und Ungenauigkeiten auf, liest sich aber recht flüssig und bietet den wichtigsten Überblick zum Beweis der fermatschen Vermutung.
Anschliessend noch eine Auflistung von Mathematikern (Évariste Galois; Johann Carl Friedrich Gauß, Gerd Faltings), welche zwar nur indirekt mit der fermatschen Vermutung zu tun haben, aber, nicht unerwähnt bleiben sollen. Ganz am Schluss widme ich mich der "Fields-Medaille".
Évariste Galois (* 25. Oktober 1811 in Bourg-la-Reine; † 31. Mai 1832 in Paris) war ein französischer Mathematiker. Er starb im Alter von nur 20 Jahren bei einem Duell, erlangte allerdings durch seine Arbeiten zur Lösung algebraischer Gleichungen, der so genannten Galoistheorie, postum Anerkennung; er hat allerdeings wenig Schriftliches von seinem Wissen hinterlassen; die Gründe für seinen frühen Tod lagen unter Anderem darin, dass er ein Anhänger der französischen Revolution gewesen sein soll.
Johann Carl Friedrich Gauß (latinisiert Carolus Fridericus Gauss; * 30. April 1777 in Braunschweig; † 23. Februar 1855 in Göttingen) war ein deutscher Mathematiker, Astronom, Geodät und Physiker mit einem breit gefächerten Feld an Interessen.
Gerd Faltings (* 28. Juli 1954 in Gelsenkirchen-Buer + ca 2008 bis 2011) ist ein deutscher Mathematiker und Träger der Fields-Medaille.
Er konnte beweisen, dass, wenn es "fermatsche Lösungstrippel" gab, diese Trippel nur für eine endliche Zahl von Exponenten und Basen gelten konnte.
Nun zur "Fields-Medaille":
Die Fields-Medaille, offizieller Name International Medal for Outstanding Discoveries in Mathematics (deutsch: Internationale Medaille für herausragende Entdeckungen in der Mathematik), ist eine der höchsten Auszeichnungen, die man als Mathematiker erhalten kann.
Die Empfänger der Medaille müssen vor dem 1. Januar des Jahres, in dem sie ausgezeichnet werden, jünger als 40 Jahre gewesen sein.
Dieser Preis gilt als eine Art "Nobelpreis" für Mathematiker; Nobelpreise gibt es nur in den Sparten Physik, Chemie, Medizin, Literatur sowie den "Friedensnobelpreis". Manche sagen, dass Nobel auch für die Mathematik einen solchen Preis einführen wollte, dies jeoch wegen einem Streit mit einem Mathematiker nicht geschah.
Die Klausel mit der Altersgrenze verhinderte zum Beispiel die Verleihung an Andrew Wiles (* 1953), dem der Beweis des Modularitätssatzes (aus dem der große fermatsche Satz folgt) erst 1993 teilweise und 1995 vollständig gelang. Wiles erhielt stattdessen auf dem ICM 1998 in Berlin eine Sonderauszeichnung der IMU, verbunden mit einer Silberplakette.
Ich möchte hervorheben, dass ich selber die wichtigsten Informationen zu diesem Thema nur durch das Internet erhalten habe (welches zum Teil widersprüchliche Angaben lieferte), und, manche Textabschnitte dort heraus einfach nur kopiert habe, allerdings nie Kopien mit allzulangen Texten, weswegen ich hoffe, hier keine urheberrechtlichen Schwierigkeiten zu bekommen.
Für die inhaltliche Richtigkeit des von mir hier Gesagtem kann ich somit also auch nur zum Teil geradestehen, zumal ich kaum die Möglichkeit zu einer "objektiven Recherche" habe; sollten sich also Fehler darin finden, so sind diese von meiner Seite aus unbeabsichtigt; keinesfalls entspricht es jedoch meiner Intention, den Ruf irgendwelcher Personen zu schmälern.
Ende: MI 22 Februar 2012
1.2) Beweisidee für die fermatsche Vermutung (Fall 1)
Anfang: Berlin 26. Nov. 09
==================================
==================================
==================================
ACHTUNG, WARNUNG:
Dieser Abschnitt ist zur Zeit in Arbeit und enthällt einige Fehler, eventuell ist er auch ganz unverständlich; nur der Anfang ist lesbar; am Besten, Sie überspringen ihn einfach!
==================================
==================================
==================================
Hier werden meine Beweisversuche der fermatschen Vermutung für den "Fall 1" vorgestellt, entweder sind sie richtig, oder aber enthalten einen elementaren Fehler, der dann aber leicht zu finden sein dürfte...........
Ich überlasse es dem Kritiker, dies zu beurteilen.
Eine Übertragung auf den "Fall 2" scheint auch recht einfach zu sein, aber, das sei zunächst dahingestellt, bei näherer Betrachtung allerdings scheint es Probleme zu geben, zumindest in meinen Augen.
Gefunden habe ich die ganze Sache am Freitag, den 11 März 2011.
Wer diesen Beweis im "Schnelldurchgang" lesen möchte, sollte nur die Kapitel "7" und "8" lesen.
==================================
==================================
==================================
Übersicht:
0) Übersicht
1) Vier Vorbemerkungen:
2) Nun zu der Methode:
3) Das pascalsche Dreieck
4) Begrifflichkeit:
5) Nun zum Zahlensystem:
6) Summenfolgendarstellung:
7) ZUSAMMENFASSUNG DES ZAHLENSYSTEMS:
8) Beweisführung
****************************
Die einzelnen Kapitel werden mit folgender Leiste voneinander getrennt:
==================================
==================================
==================================
1) Vier Vorbemerkungen:
Auf dieser Interneteite kann nicht immer alles perfekt dargestellt werden, so daß es einiger Erläuterungen bedarf:
1.1)___ Verschiedene Browser machen den Zeilenumbruch in dieser Seite an jeweils anderer Stelle, so daß der Text derart dargestellt wird, daß mathematische Ausdrücke nicht in den möglichen Bereich eines Zeilenumbruches fallen (also ärgerlicherweise in zwei oder mehr Zeilen). Der Textbereich kann auch durch Entfernen der Bilder am Seitenrand nicht vergrößert werden, weswegen meine Beweisversuche denn auch stilecht am Seitenrand niedergeschrieben wird.
1.2)___ Das Textverarbeitungsprogramm akzeptiert nur ein einziges "Leerzeichen" und stellt mehrere Blank´s als nur ein einziges dar. Drei verschiedene Leerzeichen zwischen z.B. den Buchstaben x und y werden z.b.deswegen so dargesetellt:
x___y
1.3)___Der Ausdruck (x^n) bedeutet "x hoch n" und der Ausdruck "(n_3)" bedeutet "n mit dem Index 3", "a*b". bedeutet "a mal b" und "x/y" bedeutet "x geteilt durch y", und +/- bedeutet: "Plusminus".
1.4)___Verschiedene Schriftarten/ Schriftformen/ unterstrichene Schrift oder Fettdruck sind nicht möglich.
==================================
==================================
==================================
2) Nun zu der Methode:
Hier wird das Grundprinzip einer methodischen Vorgehensweise erörtert, mittels der ich versucht habe, den "Fall 1" der fermatschen Vermutung zu beweisen, und außerdem könnte das (modifizierte) Verfahren auch auf den "Fall II" angewandt werden.
Bekannt ist zunächst , dass die "fermatsche Vermutung" (in Folge hier auch "FV" genannt) nur für teilerfremde Basen x,y und z sowie für ungerade prime Exponenten p bewiesen zu werden braucht, also nur für den Ausdruck:
x^p + y^p = z^p
"Fall 1" bedeutet, dass die Zahl xyz nicht durch p teilbar ist, bei "Fall 2" gilt:
p | xyz
Die Methode basiert auf einem Widerspruchsbeweis.
==================================
==================================
==================================
3) Das pascalsche Dreieck
Zunächst aber nun zum "pascalschen Dreieck"; mittels dieses Dreieckes, welches schon lange bekannt ist, und nach Blaise Pascal benannt worden ist, lassen sich Ausdrücke wie z.B.
(a + b)^n oder aber (x-y)^n als Summenfolge darstellen. (Die Zahlen a,b,x,y und n sind hier allesamt natürliche Zahlen).
Das pascallsche Dreieck (der obere Teil):
____________________________1______________Ebene 0
__________________________1___1____________Ebene 1
________________________1___2___1__________Ebene 2
______________________1___3___3___1________Ebene 3
____________________1___4___6___4___1______Ebene 4
__________________1___5__10___10__5___1____Ebene 5
________________1___6__15___20__15__6___1__Ebene 6
______________1___7__21___35__35__21__7___1___usw.
Die Zahlen in einer Ebene sind immer die Summe beider Zahlen der Ebene darüber.
So gilt z.B. (10 = (4 + 6)), oder aber: (15 = (10 + 5)) .
Der Sinn diese Dreieckes liegt darin, Ausdrücke wie z.B. (x + y)^3 oder aber (z - a)^4 als Summenfolgen darzustellen.
So gilt z.B.:
(x + y)^3 = (x^3) + 3*(x^2)*y + 3*x*(y^2) + (y^3)
oder aber:
(z - a)^4 = (z^4) - 4*(z^3)*a + 6*(z^2)*(a^2) - 4*z*(a^3) + (a^4)
=================================
=================================
=================================
4) Begrifflichkeit:
Ich werde bei meiner Beweisführung ein paar neue, "selbsterfundene" Begriffe einführen, welche die Erklärung vereinfachen, wie z.B. den Begriff der "Teilbarkeitsregel T", der "K-Darstellung":
------ 4.1) die "Teilbarkeitsregel T":
Gilt ggT (x,y) = 1 und ist p eine ungerade Primzahl und ist (x + y) nicht durch p teilbar, dann gilt:
(x + y) || (x^p) + (y^p)
Gilt ggT (z,y) = 1 und ist p eine ungerade Primzahl und ist (z - y) nicht durch p teilbar, dann gilt:
(z - y) || (z^p) - (y^p)
Dies erkennt man, wenn man im ersten Beispiel den Ausdruck (x^p) + (y^p) durch den Ausdruck
(x^p) + ((w -x )^p) ersetzt mit w = (x + y) und den Ausdruck ((w - x)^p) als Summenfolge mittels den Koeffizienten des pascalschen Dreieckes darstellt, und, im zweiten Beispiel den Ausdruck
(z^p) - (y^p) durch den Ausdruck ((y + b)^p) - (y^p) ersetzt mit z = ( y + b), und dann den Ausdruck ((y + b)^p) als Summenfolge mittels den Koeffizienten des pascalschen Dreieckes darstellt, denn die zwe ersten Koeffizienten einer "Ebene p" sind immer die Zahlen 1 und p.
Somit gilt dann auch:
p*(x + y) || (x^p) + (y^p)
sowie
p*(z - y) || (z^p) - (y^p)
wenn (x + y) oder aber (z - y) durch p teilbar wären.
------ 4.2) die"K-Darstellung:":
Unter "K-Darstellung" verstehe ich, dass, taucht in einer Summenfolge der Ausdruck k*d*(z^t) auf, und die Zahlen k und d die als Buchstaben dargestellte Zahl z nicht mehr enthalten, und außerdem auch gilt:
z = (x + a), der Ausdruck k*d*(z^t) dargestellt wird als k*d*((x + a)^t) und der Ausdruck
(x + a)^t dabei als Summenfolge mittels der Koeffizienten des pascalschen Dreieckes dargestellt wird. Ein Beispiel:
15*d*(z^3) = 15*d*((x + a)^3) wird k-dargestellt als:
15*d*(x^3) + 15*d*3*(x^2)*a + 15*d*3*x*(a^2) + 15*d*(a^3)
Die "Sprachregelung" lautet dann: "(z^t) wird k-dargestellt als ((x + a)^t)".
Ist der Wert (x + a) schon vorhanden, aber, noch nicht als Summenfolge dargestellt, lautet die Ausdrucksweise: "Die Zahl ((x + a)^t) wird k-dargestellt"
------ 4.3) Die "Summenfolgedarstellung":
Noch offen, Erklärung folgt aber weiter unten
Folgende Begriffe werden zur Beweisführung nicht gebraucht und werden nur der Komplettheit wegen erörtert::
------ 4.4) Die "B-Darstellung":
Die B-Darstellung beschreibt, aus welchen als Buchsteben dargestelltern Zahlen eine Summenfolge besteht.
------ 4.5) "obere und untere Primzahlen":
In dem Wert x^g - y^g (mit g als geradem Exponenten) nenne ich die Teiler dieses Wertes, die durch (x+y)*(x-y) teilbar sind, die "unteren Primzahlen", der rest sind die "oberen Primzahlen".
Für u als ungeraden Exponenten finden sich für den Wert
x^u +/- y^u
die unteren Primzahlen im Wert (x +/- y)
------ 4.6) "Korrekturwert":
Ist eine Zahl durch eine Zahl mit einer bestimmten Vielheit teilbar, bestimmt der "Korrekturwert" jene Zahl, mittes der diese Zahl mit einer größeren Vielheit teilbar ist. Beispiel:
Wir nehmen die Zahlen x und y mit w = (x + y)mit p als ungerader Primzahl und dann die Zahl:
x^p + y^p
Es gilt nun:
(p^2) | (w^p) - p*(w^(p-1))*y
Solldiese Zahl dann aber durch (p^3) teilbar sein, muss ein Korrekturwert hinzugefügt werden:
(p^3) | (w^p) - p*(w^(p-1))*y + ((p-1)/2)*(w^(p-2))*(y^2)
Der Wert ((p-1)/2)*(w^(p-2))*(y^2) ist dann der Korrekturwert.
------ 4.7) "effektiver Exponent:
Noch offen
------ 4.8) "Summenfolgedarstellung":
Sie auch Kapitel 6; der Wert (x^p) + (y^p) kann mit q = (p-1) als Summenfolge dargestellt werden:
x^q - (x^(q-1))*y + (x^(q-2))*(y^2)..... - x*(y^(p-1)) + (y^q)
Analoges gilt für die Subtraktion von Potenzen.
==================================
==================================
==================================
5) Nun zum Zahlensystem:
Zunächst gilt:
(x + y)^p > (x^p) + (y^p), und, somit müsste, wenn gelten würde:
(x^p) + (y^p) = (z^p) , dann auch gelten:
(x + y)^p > (z^p) und somit: (x + y) > z und dann auch gelten
c > 0 mit (c = (x + y) - z).
Nun soll gelten:
(x + y) = w
(w - z) = c
(z - x) = a
(z - y) = b
Damit gilt dann auch:
(y - a) = c
(x - b) = c
da nun gilt im Fall 1 (aufgrund der Teilbarkeitsregel T):
w || (x^p) + (y^p) , als auch:
a || (z^p) - (x^p) , sowie:
b || (z^p) - (y^p) ,
Muss auch gelten:
w || (z^p)
a || (y^p)
b || (x^p)
Da sich eine p-te Potenz aber nur so als Produkt zweier teilerfremden Zahlen darstellen lässt, wenn beide dieser Zahlen p-te Potenzen sind, müssen die Zahlen w; a und b alle p-te Potenzen sein.
Es gilt somit:
w = (h^p) mit (z^p) = w(v^p) und z = vh
a = (r^p) mit (y^p) = a(n^p) und y = r*n
b = (s^p) mit (x^p) = b(m^p) und x = sm
Da nun gilt:
y - a = x - b = w - z = c___, gilt auch:
r*n - (r^p) = sm - (s^p) = (h^p) - hv = c, gilt auch:
hrs || c_____, und somit gilt:
c = fhrs___und___(c^p) = (f^p)wab
==================================
==================================
==================================
6) Summenfolgendarstellung:
Da nun gilt:
(n^p) = ((z^p) - (x^p))/a
(m^p) = ((z^p) - (y^p))/b
(v^p) = ((x^p) + (y^p))/w
gilt auch:
(n^p) = (z^q) + (z^(q-1))*x +........ + z*(x^(q-1)) + (x^q))
(m^p) = (z^q) + (z^(q-1))*y +........ + z*(y^(q-1)) + (y^q))
(v^p) = (x^q) - (x^(q-1))*y -........ - x*(y^(q-1)) + (y^q))
mit q = (p-1).
Das Ganze soll mal am Beispiel des Falles p = 5 verdeutlicht werden:
(v^5) = (x^4) - (x^3)*y + (x^2)*(y^2) - x*(y^3) + (y^4)
Da nun gilt. w = (x + y), kann man die linke Seite mit w,
und die rechte Seite mit (x + y) multiplizieren und erhällt:
w*(v^5) = (x^5) + (y^5)
==================================
==================================
==================================
7) ZUSAMMENFASSUNG DES ZAHLENSYSTEMS:
(x + y) = w
(w - z) = c
(z - x) = a
(z - y) = b
(y - a) = c
(x - b) = c
x = sm
y = r*n
z = vh
w = (h^p)
a = (r^p)
b = (s^p)
(z^p) = w*(v^p)
(y^p) = a*(n^p)
(x^p) = b*(m^p)
c = fhrs
(c^p) = (f^p)wab
q = (p-1)
Die Zahlen d,t und j und k finden freie Verwendung, und haben je nach Einsatz verschiedene Bedeutung.
g steht allgemein für einen geraden, und u allgemein für einen ungeraden Exponenten.
Die Zahlen f,h,r und s sind jeweils paarweise zueinander teilerfremd.
==================================
==================================
==================================
8) Beweisführung:
Zunächst wird davon ausgegangen (der Beweis basiert auf dem Prinzip des Widerspruchsbeweises), dass gilt:
x^p + y^p = z^p
Da nun, ist t eine natürliche Zahl, immer gilt:
p | (t^p) - t
(was unter Anderem aus dem kleinen fermatschen Satz hervorgeht), kann man zu dem Ausdruck
x^p + y^p - z^p
die durch p teilbaren Ausdrücke
x - (x^p) + y - (y^p) + (z^p) - z
addieren, und erhällt nun den durch p teilbaren Ausdruck
p | x + y - z = c
Somit ist c immer durch p teilbar, und, im Fall 1, weil gilt:
c = fhrs
gilt auch:
p | f
weil die Zahlen h,r und s nur Primfaktoren von z,y und x enthalten.
Da nun gilt:
w - z = c ___ und ___ y - a = c ___ und ___ x - b = c
Gilt nun auch:
p | (h^p) - v*h = w - z
p | n*r - (r^p) = y - a
p | m*s - (s^p) = x - b
und somit auch:
p | (h^q) - v
p | n - (r^q)
p | m - (s^q)
Da nun h,r und s teilerfremd zu p sind, sind die drei Zahlen
h^q - 1
r^q - 1
s^q - 1
Immer durch p teilbar, was aus dem kleinen fermatschen Satz hervorgeht, und somit auch die drei Zahlen
v - 1
n - 1
m - 1
Durch p teilbar. Damit gilt aufgrund der "Teilbarkeitsregel T" dann:
(p^2) | (v^p) - 1
(p^2) | (n^p) - 1
(p^2) | (m^p) - 1
Somit kann man zu dem Wert
x^p + y^p - z^p = 0 = b*(m^p) + a*(n^p) - w*(v^p)
Die drei durch (p^2) teilbaren Werte
(p^2) | b*(1 - (m^p))
(p^2) | a*(1 - (n^p))
(p^2) | w*((v^p) - 1)
addieren und erhällt nun den durch (p^2) teilbaren Wert:
(p^2) | - w + a + b = - 2*c
und somit gilt dann:
(p^2) | c
Nun beginnt die eigentliche Beweisführung:
Zunächst gilt:
(y^p) = a*(n^p) = ((c+a)^p)
Die Zahl y wird dann K - dargestellt als Summenfolge mit den Zahlen c und a, und dann wird die ganze Sache durch a geteilt, anschliessend wird eine K-Darstellung von a als (y - c) gemacht. Man erhällt dann eine Darstellung von (n^p); die Zahl (c^p)/a ist dann gleich (f^p)*b*w.
BEISPIEL p = 5:
(n^5) - (y^4) - c*(y^3) - (c^2)*(y^2) - (c^3)*y - (c^4) - (f^5)*b*w = 0
Damit gilt nun mit (2^k) || c :
(p^(2*k)) | (n^5) - (y^4) - c*(y^3)
Die Weiterführung des Beweisprinzipes wird nun am Beispiel (p=5) weitergeführt.
Nun wird eine Summenfolgedarstellung des Wertes (n^5) gemacht, und, es gilt nun (Dieser Ausdruck beansprucht zwei Zeilen):
(p^(2*k)) | - (y^4) - c*(y^3)
(x^4) + z*(x^3) + (z^2)*(x^2) + (z^3)*x + (z^4)
Dann wird eine K-Darstellung von z als (w - c) gemacht, und alle durch (c^2) und somit auch durch (p^(2*k)) teilbaren Werte eliminiert, es gilt nun (dieser Ausdruck beansprucht auch zwei Zeilen):
(p^(2*k) | 5*(x^4) + 10*(x^3)*y + 10*(x^2)*(y^3) + 5*x*(y^3)
- 10*c*(x^3) - 20*c*(x^2)*y - 15*c*x*(y^2) - 5*c*(y^3)
Dies lässt sich auch darstellen als:
((w^5) - (x^5) - (y^5))/y
- 10*c*(x^2)*(x+y) - 10*c*x*y*(x+y) - 5*c*(y^2)*(x+y)
Da nun gilt: (x+y) = w, lässt sich dieser Wert aber nun auch darstellen als
((w^5) - (x^5) - (y^5))/y
- c*w*((w^5) - (x^5) - (y^5) - 5*((x^4)*y))/(x*(y^2))
Dieser Ausdruck wird mit x*(y^2) multipliziert, es entsteht der durch (p^2) teilbare Ausdruck A1:
((w^5) - (x^5) - (y^5))*x*(y^2)
- c*w*((w^5) - (x^5) - (y^5))*y - 5*(x^4)*(y^2)
Aus diesem Ausdruck A1 geht hervor, dass gilt:
(p^k) | (w^5) - (x^5) - (y^5)
Deswegen wird nun zu A1 der durch (p^(2*k)) teilbare Wert
c*w*((w^5) - (x^5) - (y^5))*y
addiert, und, es gilt nun:
(p^(2*k)) | ((w^5) - (x^5) - (y^5))*x*(y^2) + 5*c*w*(x^4)*(y^2)
Nun wird der ganze Wert durch die zu p teilerfremden Zahlen x*(y^2) dividiert, und, vom Ausdruck (w^5) eine K-Darstellung mit (w^5) = ((z+c)^5)gemacht, dann der Ausdruck
(z^5) - (x^5) - (y^5) abgezogen sowie alle durch (c^2) teilbaren Zahlen eliminiert. Es gilt nun:
(p^(2*k)) | 5*c*(z^4) + 5*c*w*(x^3)
Damit gilt nun:
(p^(k-1)) | (z^4) + w*(x^3)
und auch gilt: k > 1, gilt somit:
p | (z^4) + w*(x^3)
Dazu wird der durch c und somit p teilbare Wert
(z - w)*(x^3)
addiert und durch das zu p teilerfremde z geteilt:
p | (z^3) + (x^3)
Dieser Ausdruck wird mit x multipliziert und dazu der aufgrund des kleinen fermatschen Satz durch p teilbare Wert
(z^4) - (x^4)
addiert; dieser Wert wird durch das zu p teilerfremde (z^3) geteilt, und, es gilt nun:
p | z + x
Da nun auch gilt:
(p^(2*k)) || (m^p) - (x^q) - c*(x^(q-1))
, kann man beweisen, dass nun auch gelten muss:
p | z + y
(Man kann die Umformungen genauso begehen, und muss nur die Zahlen x und y vertauschen)
Somit gilt dann:
p | 2*z + x + y
Dazu wird der durch c und somit auch durch p teilbare Wert
p | z - x - y
addiert, und, es gilt nun:
p | 3*z
und somit:
p | 3
Natürlich hat dieser Beweis nicht für p=3 Gültigkeit, und, ist nur dann korrekt, wenn er sich auf alle p>3 transformieren lässt.
==================================
==================================
==================================
Ende: Berlin DO 22 März 2012
==================================
==================================
==================================
ACHTUNG, WARNUNG:
Dieser Abschnitt ist zur Zeit in Arbeit und enthällt einige Fehler, eventuell ist er auch ganz unverständlich; nur der Anfang ist lesbar; am Besten, Sie überspringen ihn einfach!
==================================
==================================
==================================
Hier werden meine Beweisversuche der fermatschen Vermutung für den "Fall 1" vorgestellt, entweder sind sie richtig, oder aber enthalten einen elementaren Fehler, der dann aber leicht zu finden sein dürfte...........
Ich überlasse es dem Kritiker, dies zu beurteilen.
Eine Übertragung auf den "Fall 2" scheint auch recht einfach zu sein, aber, das sei zunächst dahingestellt, bei näherer Betrachtung allerdings scheint es Probleme zu geben, zumindest in meinen Augen.
Gefunden habe ich die ganze Sache am Freitag, den 11 März 2011.
Wer diesen Beweis im "Schnelldurchgang" lesen möchte, sollte nur die Kapitel "7" und "8" lesen.
==================================
==================================
==================================
Übersicht:
0) Übersicht
1) Vier Vorbemerkungen:
2) Nun zu der Methode:
3) Das pascalsche Dreieck
4) Begrifflichkeit:
5) Nun zum Zahlensystem:
6) Summenfolgendarstellung:
7) ZUSAMMENFASSUNG DES ZAHLENSYSTEMS:
8) Beweisführung
****************************
Die einzelnen Kapitel werden mit folgender Leiste voneinander getrennt:
==================================
==================================
==================================
1) Vier Vorbemerkungen:
Auf dieser Interneteite kann nicht immer alles perfekt dargestellt werden, so daß es einiger Erläuterungen bedarf:
1.1)___ Verschiedene Browser machen den Zeilenumbruch in dieser Seite an jeweils anderer Stelle, so daß der Text derart dargestellt wird, daß mathematische Ausdrücke nicht in den möglichen Bereich eines Zeilenumbruches fallen (also ärgerlicherweise in zwei oder mehr Zeilen). Der Textbereich kann auch durch Entfernen der Bilder am Seitenrand nicht vergrößert werden, weswegen meine Beweisversuche denn auch stilecht am Seitenrand niedergeschrieben wird.
1.2)___ Das Textverarbeitungsprogramm akzeptiert nur ein einziges "Leerzeichen" und stellt mehrere Blank´s als nur ein einziges dar. Drei verschiedene Leerzeichen zwischen z.B. den Buchstaben x und y werden z.b.deswegen so dargesetellt:
x___y
1.3)___Der Ausdruck (x^n) bedeutet "x hoch n" und der Ausdruck "(n_3)" bedeutet "n mit dem Index 3", "a*b". bedeutet "a mal b" und "x/y" bedeutet "x geteilt durch y", und +/- bedeutet: "Plusminus".
1.4)___Verschiedene Schriftarten/ Schriftformen/ unterstrichene Schrift oder Fettdruck sind nicht möglich.
==================================
==================================
==================================
2) Nun zu der Methode:
Hier wird das Grundprinzip einer methodischen Vorgehensweise erörtert, mittels der ich versucht habe, den "Fall 1" der fermatschen Vermutung zu beweisen, und außerdem könnte das (modifizierte) Verfahren auch auf den "Fall II" angewandt werden.
Bekannt ist zunächst , dass die "fermatsche Vermutung" (in Folge hier auch "FV" genannt) nur für teilerfremde Basen x,y und z sowie für ungerade prime Exponenten p bewiesen zu werden braucht, also nur für den Ausdruck:
x^p + y^p = z^p
"Fall 1" bedeutet, dass die Zahl xyz nicht durch p teilbar ist, bei "Fall 2" gilt:
p | xyz
Die Methode basiert auf einem Widerspruchsbeweis.
==================================
==================================
==================================
3) Das pascalsche Dreieck
Zunächst aber nun zum "pascalschen Dreieck"; mittels dieses Dreieckes, welches schon lange bekannt ist, und nach Blaise Pascal benannt worden ist, lassen sich Ausdrücke wie z.B.
(a + b)^n oder aber (x-y)^n als Summenfolge darstellen. (Die Zahlen a,b,x,y und n sind hier allesamt natürliche Zahlen).
Das pascallsche Dreieck (der obere Teil):
____________________________1______________Ebene 0
__________________________1___1____________Ebene 1
________________________1___2___1__________Ebene 2
______________________1___3___3___1________Ebene 3
____________________1___4___6___4___1______Ebene 4
__________________1___5__10___10__5___1____Ebene 5
________________1___6__15___20__15__6___1__Ebene 6
______________1___7__21___35__35__21__7___1___usw.
Die Zahlen in einer Ebene sind immer die Summe beider Zahlen der Ebene darüber.
So gilt z.B. (10 = (4 + 6)), oder aber: (15 = (10 + 5)) .
Der Sinn diese Dreieckes liegt darin, Ausdrücke wie z.B. (x + y)^3 oder aber (z - a)^4 als Summenfolgen darzustellen.
So gilt z.B.:
(x + y)^3 = (x^3) + 3*(x^2)*y + 3*x*(y^2) + (y^3)
oder aber:
(z - a)^4 = (z^4) - 4*(z^3)*a + 6*(z^2)*(a^2) - 4*z*(a^3) + (a^4)
=================================
=================================
=================================
4) Begrifflichkeit:
Ich werde bei meiner Beweisführung ein paar neue, "selbsterfundene" Begriffe einführen, welche die Erklärung vereinfachen, wie z.B. den Begriff der "Teilbarkeitsregel T", der "K-Darstellung":
------ 4.1) die "Teilbarkeitsregel T":
Gilt ggT (x,y) = 1 und ist p eine ungerade Primzahl und ist (x + y) nicht durch p teilbar, dann gilt:
(x + y) || (x^p) + (y^p)
Gilt ggT (z,y) = 1 und ist p eine ungerade Primzahl und ist (z - y) nicht durch p teilbar, dann gilt:
(z - y) || (z^p) - (y^p)
Dies erkennt man, wenn man im ersten Beispiel den Ausdruck (x^p) + (y^p) durch den Ausdruck
(x^p) + ((w -x )^p) ersetzt mit w = (x + y) und den Ausdruck ((w - x)^p) als Summenfolge mittels den Koeffizienten des pascalschen Dreieckes darstellt, und, im zweiten Beispiel den Ausdruck
(z^p) - (y^p) durch den Ausdruck ((y + b)^p) - (y^p) ersetzt mit z = ( y + b), und dann den Ausdruck ((y + b)^p) als Summenfolge mittels den Koeffizienten des pascalschen Dreieckes darstellt, denn die zwe ersten Koeffizienten einer "Ebene p" sind immer die Zahlen 1 und p.
Somit gilt dann auch:
p*(x + y) || (x^p) + (y^p)
sowie
p*(z - y) || (z^p) - (y^p)
wenn (x + y) oder aber (z - y) durch p teilbar wären.
------ 4.2) die"K-Darstellung:":
Unter "K-Darstellung" verstehe ich, dass, taucht in einer Summenfolge der Ausdruck k*d*(z^t) auf, und die Zahlen k und d die als Buchstaben dargestellte Zahl z nicht mehr enthalten, und außerdem auch gilt:
z = (x + a), der Ausdruck k*d*(z^t) dargestellt wird als k*d*((x + a)^t) und der Ausdruck
(x + a)^t dabei als Summenfolge mittels der Koeffizienten des pascalschen Dreieckes dargestellt wird. Ein Beispiel:
15*d*(z^3) = 15*d*((x + a)^3) wird k-dargestellt als:
15*d*(x^3) + 15*d*3*(x^2)*a + 15*d*3*x*(a^2) + 15*d*(a^3)
Die "Sprachregelung" lautet dann: "(z^t) wird k-dargestellt als ((x + a)^t)".
Ist der Wert (x + a) schon vorhanden, aber, noch nicht als Summenfolge dargestellt, lautet die Ausdrucksweise: "Die Zahl ((x + a)^t) wird k-dargestellt"
------ 4.3) Die "Summenfolgedarstellung":
Noch offen, Erklärung folgt aber weiter unten
Folgende Begriffe werden zur Beweisführung nicht gebraucht und werden nur der Komplettheit wegen erörtert::
------ 4.4) Die "B-Darstellung":
Die B-Darstellung beschreibt, aus welchen als Buchsteben dargestelltern Zahlen eine Summenfolge besteht.
------ 4.5) "obere und untere Primzahlen":
In dem Wert x^g - y^g (mit g als geradem Exponenten) nenne ich die Teiler dieses Wertes, die durch (x+y)*(x-y) teilbar sind, die "unteren Primzahlen", der rest sind die "oberen Primzahlen".
Für u als ungeraden Exponenten finden sich für den Wert
x^u +/- y^u
die unteren Primzahlen im Wert (x +/- y)
------ 4.6) "Korrekturwert":
Ist eine Zahl durch eine Zahl mit einer bestimmten Vielheit teilbar, bestimmt der "Korrekturwert" jene Zahl, mittes der diese Zahl mit einer größeren Vielheit teilbar ist. Beispiel:
Wir nehmen die Zahlen x und y mit w = (x + y)mit p als ungerader Primzahl und dann die Zahl:
x^p + y^p
Es gilt nun:
(p^2) | (w^p) - p*(w^(p-1))*y
Solldiese Zahl dann aber durch (p^3) teilbar sein, muss ein Korrekturwert hinzugefügt werden:
(p^3) | (w^p) - p*(w^(p-1))*y + ((p-1)/2)*(w^(p-2))*(y^2)
Der Wert ((p-1)/2)*(w^(p-2))*(y^2) ist dann der Korrekturwert.
------ 4.7) "effektiver Exponent:
Noch offen
------ 4.8) "Summenfolgedarstellung":
Sie auch Kapitel 6; der Wert (x^p) + (y^p) kann mit q = (p-1) als Summenfolge dargestellt werden:
x^q - (x^(q-1))*y + (x^(q-2))*(y^2)..... - x*(y^(p-1)) + (y^q)
Analoges gilt für die Subtraktion von Potenzen.
==================================
==================================
==================================
5) Nun zum Zahlensystem:
Zunächst gilt:
(x + y)^p > (x^p) + (y^p), und, somit müsste, wenn gelten würde:
(x^p) + (y^p) = (z^p) , dann auch gelten:
(x + y)^p > (z^p) und somit: (x + y) > z und dann auch gelten
c > 0 mit (c = (x + y) - z).
Nun soll gelten:
(x + y) = w
(w - z) = c
(z - x) = a
(z - y) = b
Damit gilt dann auch:
(y - a) = c
(x - b) = c
da nun gilt im Fall 1 (aufgrund der Teilbarkeitsregel T):
w || (x^p) + (y^p) , als auch:
a || (z^p) - (x^p) , sowie:
b || (z^p) - (y^p) ,
Muss auch gelten:
w || (z^p)
a || (y^p)
b || (x^p)
Da sich eine p-te Potenz aber nur so als Produkt zweier teilerfremden Zahlen darstellen lässt, wenn beide dieser Zahlen p-te Potenzen sind, müssen die Zahlen w; a und b alle p-te Potenzen sein.
Es gilt somit:
w = (h^p) mit (z^p) = w(v^p) und z = vh
a = (r^p) mit (y^p) = a(n^p) und y = r*n
b = (s^p) mit (x^p) = b(m^p) und x = sm
Da nun gilt:
y - a = x - b = w - z = c___, gilt auch:
r*n - (r^p) = sm - (s^p) = (h^p) - hv = c, gilt auch:
hrs || c_____, und somit gilt:
c = fhrs___und___(c^p) = (f^p)wab
==================================
==================================
==================================
6) Summenfolgendarstellung:
Da nun gilt:
(n^p) = ((z^p) - (x^p))/a
(m^p) = ((z^p) - (y^p))/b
(v^p) = ((x^p) + (y^p))/w
gilt auch:
(n^p) = (z^q) + (z^(q-1))*x +........ + z*(x^(q-1)) + (x^q))
(m^p) = (z^q) + (z^(q-1))*y +........ + z*(y^(q-1)) + (y^q))
(v^p) = (x^q) - (x^(q-1))*y -........ - x*(y^(q-1)) + (y^q))
mit q = (p-1).
Das Ganze soll mal am Beispiel des Falles p = 5 verdeutlicht werden:
(v^5) = (x^4) - (x^3)*y + (x^2)*(y^2) - x*(y^3) + (y^4)
Da nun gilt. w = (x + y), kann man die linke Seite mit w,
und die rechte Seite mit (x + y) multiplizieren und erhällt:
w*(v^5) = (x^5) + (y^5)
==================================
==================================
==================================
7) ZUSAMMENFASSUNG DES ZAHLENSYSTEMS:
(x + y) = w
(w - z) = c
(z - x) = a
(z - y) = b
(y - a) = c
(x - b) = c
x = sm
y = r*n
z = vh
w = (h^p)
a = (r^p)
b = (s^p)
(z^p) = w*(v^p)
(y^p) = a*(n^p)
(x^p) = b*(m^p)
c = fhrs
(c^p) = (f^p)wab
q = (p-1)
Die Zahlen d,t und j und k finden freie Verwendung, und haben je nach Einsatz verschiedene Bedeutung.
g steht allgemein für einen geraden, und u allgemein für einen ungeraden Exponenten.
Die Zahlen f,h,r und s sind jeweils paarweise zueinander teilerfremd.
==================================
==================================
==================================
8) Beweisführung:
Zunächst wird davon ausgegangen (der Beweis basiert auf dem Prinzip des Widerspruchsbeweises), dass gilt:
x^p + y^p = z^p
Da nun, ist t eine natürliche Zahl, immer gilt:
p | (t^p) - t
(was unter Anderem aus dem kleinen fermatschen Satz hervorgeht), kann man zu dem Ausdruck
x^p + y^p - z^p
die durch p teilbaren Ausdrücke
x - (x^p) + y - (y^p) + (z^p) - z
addieren, und erhällt nun den durch p teilbaren Ausdruck
p | x + y - z = c
Somit ist c immer durch p teilbar, und, im Fall 1, weil gilt:
c = fhrs
gilt auch:
p | f
weil die Zahlen h,r und s nur Primfaktoren von z,y und x enthalten.
Da nun gilt:
w - z = c ___ und ___ y - a = c ___ und ___ x - b = c
Gilt nun auch:
p | (h^p) - v*h = w - z
p | n*r - (r^p) = y - a
p | m*s - (s^p) = x - b
und somit auch:
p | (h^q) - v
p | n - (r^q)
p | m - (s^q)
Da nun h,r und s teilerfremd zu p sind, sind die drei Zahlen
h^q - 1
r^q - 1
s^q - 1
Immer durch p teilbar, was aus dem kleinen fermatschen Satz hervorgeht, und somit auch die drei Zahlen
v - 1
n - 1
m - 1
Durch p teilbar. Damit gilt aufgrund der "Teilbarkeitsregel T" dann:
(p^2) | (v^p) - 1
(p^2) | (n^p) - 1
(p^2) | (m^p) - 1
Somit kann man zu dem Wert
x^p + y^p - z^p = 0 = b*(m^p) + a*(n^p) - w*(v^p)
Die drei durch (p^2) teilbaren Werte
(p^2) | b*(1 - (m^p))
(p^2) | a*(1 - (n^p))
(p^2) | w*((v^p) - 1)
addieren und erhällt nun den durch (p^2) teilbaren Wert:
(p^2) | - w + a + b = - 2*c
und somit gilt dann:
(p^2) | c
Nun beginnt die eigentliche Beweisführung:
Zunächst gilt:
(y^p) = a*(n^p) = ((c+a)^p)
Die Zahl y wird dann K - dargestellt als Summenfolge mit den Zahlen c und a, und dann wird die ganze Sache durch a geteilt, anschliessend wird eine K-Darstellung von a als (y - c) gemacht. Man erhällt dann eine Darstellung von (n^p); die Zahl (c^p)/a ist dann gleich (f^p)*b*w.
BEISPIEL p = 5:
(n^5) - (y^4) - c*(y^3) - (c^2)*(y^2) - (c^3)*y - (c^4) - (f^5)*b*w = 0
Damit gilt nun mit (2^k) || c :
(p^(2*k)) | (n^5) - (y^4) - c*(y^3)
Die Weiterführung des Beweisprinzipes wird nun am Beispiel (p=5) weitergeführt.
Nun wird eine Summenfolgedarstellung des Wertes (n^5) gemacht, und, es gilt nun (Dieser Ausdruck beansprucht zwei Zeilen):
(p^(2*k)) | - (y^4) - c*(y^3)
(x^4) + z*(x^3) + (z^2)*(x^2) + (z^3)*x + (z^4)
Dann wird eine K-Darstellung von z als (w - c) gemacht, und alle durch (c^2) und somit auch durch (p^(2*k)) teilbaren Werte eliminiert, es gilt nun (dieser Ausdruck beansprucht auch zwei Zeilen):
(p^(2*k) | 5*(x^4) + 10*(x^3)*y + 10*(x^2)*(y^3) + 5*x*(y^3)
- 10*c*(x^3) - 20*c*(x^2)*y - 15*c*x*(y^2) - 5*c*(y^3)
Dies lässt sich auch darstellen als:
((w^5) - (x^5) - (y^5))/y
- 10*c*(x^2)*(x+y) - 10*c*x*y*(x+y) - 5*c*(y^2)*(x+y)
Da nun gilt: (x+y) = w, lässt sich dieser Wert aber nun auch darstellen als
((w^5) - (x^5) - (y^5))/y
- c*w*((w^5) - (x^5) - (y^5) - 5*((x^4)*y))/(x*(y^2))
Dieser Ausdruck wird mit x*(y^2) multipliziert, es entsteht der durch (p^2) teilbare Ausdruck A1:
((w^5) - (x^5) - (y^5))*x*(y^2)
- c*w*((w^5) - (x^5) - (y^5))*y - 5*(x^4)*(y^2)
Aus diesem Ausdruck A1 geht hervor, dass gilt:
(p^k) | (w^5) - (x^5) - (y^5)
Deswegen wird nun zu A1 der durch (p^(2*k)) teilbare Wert
c*w*((w^5) - (x^5) - (y^5))*y
addiert, und, es gilt nun:
(p^(2*k)) | ((w^5) - (x^5) - (y^5))*x*(y^2) + 5*c*w*(x^4)*(y^2)
Nun wird der ganze Wert durch die zu p teilerfremden Zahlen x*(y^2) dividiert, und, vom Ausdruck (w^5) eine K-Darstellung mit (w^5) = ((z+c)^5)gemacht, dann der Ausdruck
(z^5) - (x^5) - (y^5) abgezogen sowie alle durch (c^2) teilbaren Zahlen eliminiert. Es gilt nun:
(p^(2*k)) | 5*c*(z^4) + 5*c*w*(x^3)
Damit gilt nun:
(p^(k-1)) | (z^4) + w*(x^3)
und auch gilt: k > 1, gilt somit:
p | (z^4) + w*(x^3)
Dazu wird der durch c und somit p teilbare Wert
(z - w)*(x^3)
addiert und durch das zu p teilerfremde z geteilt:
p | (z^3) + (x^3)
Dieser Ausdruck wird mit x multipliziert und dazu der aufgrund des kleinen fermatschen Satz durch p teilbare Wert
(z^4) - (x^4)
addiert; dieser Wert wird durch das zu p teilerfremde (z^3) geteilt, und, es gilt nun:
p | z + x
Da nun auch gilt:
(p^(2*k)) || (m^p) - (x^q) - c*(x^(q-1))
, kann man beweisen, dass nun auch gelten muss:
p | z + y
(Man kann die Umformungen genauso begehen, und muss nur die Zahlen x und y vertauschen)
Somit gilt dann:
p | 2*z + x + y
Dazu wird der durch c und somit auch durch p teilbare Wert
p | z - x - y
addiert, und, es gilt nun:
p | 3*z
und somit:
p | 3
Natürlich hat dieser Beweis nicht für p=3 Gültigkeit, und, ist nur dann korrekt, wenn er sich auf alle p>3 transformieren lässt.
==================================
==================================
==================================
Ende: Berlin DO 22 März 2012
Freitag, 7. Januar 2011
1.3) Über Wieferich und Mirimanoff - Primzahlen
Anfang: MO 24. Januar 2011
****************************
Kapitelübersicht:
1) Was sind Wieferich und Mirimanoff Primzahlen?
2) Wieviele dieser Primzahlen gibt es?
3) Die ersten Ansätze einer Methode zur Beweisführung und deren Kritik
4) Kritik dieser Methode
5) Noch ein Beweisindikator
6) Kurzintermezzo
7) Eine Methode, die nachweislich nicht funktioniert
8) Erste Ansätze zu einem funktionierenden Beweis
9) Ein interessanter Beweisansatz
10) Ein mißlungener Beweisansatz
11) Der Rest vom Schützenfest
****************************
****************************
****************************
1) Was sind Wieferich und Mirimanoff Primzahlen?
Im Jahre 1909 konnte der Mathematiker Arthur Wieferich für den Fall 1 der fermatschen Vermutung beweisen, dass der Exponent p (die fermatsche Vermutung braucht nur für ungerade prime Exponenten bewiesen zu werden) eine Wieferich-Primzahl sein muss, das heisst, dass gilt:
(p^2) | (2^(p-1)) - 1
Es gibt nur zwei bekannte Wieferich Primzahlen, nämlich die 3511 und die 1093. Sollte es noch mehr geben, müssen sie sehr groß sein, siehe den Link links auf dieser Seite, der hier noch einmal wiederholt wird:
http://books.google.de/books?id=-nEM9ZVr4CsC&pg=PA237&lpg=PA237&dq=Mirimanoff+Primzahl&source=bl&ots=pGk-zUiTBa&sig=UPWvBoRW9I3Wv2CbXosdPORun5A&hl=de&ei=rflGTa68CMWOswag9bGzDg&sa=X&oi=book_result&ct=result&resnum=9&ved=0CDUQ6AEwCA#v=onepage&q=Mirimanoff%20Primzahl&f=false
Im Jahre 1910 konnte dann Dimitry Mirimanoff beweisen, dass für den Fall 1 der fermatschen Vermutung auch gelten muss:
(p^2) | (3^(p-1)) - 1
Die Primzahl 11 ist z.B. eine solche "Mirimanoff - Primzahl" (eine eigene Wortkreation von mir). Die beiden bekannten Wieferich - Primzahlen sind übrigends keine Mirimanoff - Primzahlen.
Wer nun beweisen kann, dass eine Wieferich-Primuzahl niemals Mirimanoff-Primzahl sein kann, hätte also den Fall 1 der fermatschen Vermutung bewiesen, ebenso wie jene These, dass es nur zwei Wieferich - Primzahlen (die 1093 und die 3511) gibt, denn für jede einzelne Primzahl als Exponent kann die fermatsche Vermutung mit speziellen Methoden bewiesen werden.
****************************
****************************
****************************
2) Wieviele dieser Primzahlen gibt es?
Es lässt sich auch beweisen, dass es zwischen 0 und (p^2) immer genau (p-1) Zahlen n gibt, für die gilt:
(p^2) | n^(p-1) - 1
Dies geht so:
Man definiert (p-1) Gruppen, mit je p Zahlen x, die nicht durch p teilbar sind mit jeweils x<(p^2), für die gilt, dass innerhalb einer Gruppe, seien zwei Zahlen j und k konkrete Zahlen der Variable x, immer gilt:
p | j-k .
Damit gilt aufgrund des kleinen fermatschen Satzes mit q=(p-1):
p | j^q - k^q
Würde aber nun gelten:
(p^2) | j^q - k^q
, dann könnte man diesen Wert mit k multiplizieren und die durch (p^2) teilbare Zahl
(k^p) - (j^p)
addieren; es würde somit gelten:
(p^2) | (j^q)*(k - j)
, was aber nicht sein kann, da j zu p teilerfremd ist, und es gilt:
p || (k-j)
Somit lässt sich für jede Zahl x aus einer der p Zahlen umfassenden Gruppe sagen:
(p^2) | x^q - 1 - a*p
Mit a < p und einem für jede Zahl x innerhalb einer Gruppe jeweils anderen Wert für a, so dass in jeder der (p-1) Gruppen der Wert (a=0) genau einmal vorkommt, und, somit gilt für genau (p-1) Zahlen x mit x>(p^2) gilt:
(p^2) | x^(p-1) - 1
Bei p = 5 lauten diese 4 (bzw. (p-1)) Zahlen z.B.
1, 7, 18, 24
, für p = 11 lauten sie:
1, 3, 9, 27, 40, 81, 94, 112, 118, 120
Logischerweise sind die Zahlen 1 und ((p^2)-1) immer vorhanden, und auch ansonsten ist eine Symmetrie da; immer, wenn gilt:
(p^2) | n^q - 1
, auch gelten muss:
(p^2) | ((p^2) - n)^q - (n^q)
, da letzterer Wert immer durch die Summe der Basen teilbar ist, und somit gilt auch:
(p^2) | ((p^2) - n)^q - 1
Es stellt sich die (ungeklärte) Frage*, ob es unendliche viele Primzahlen p gibt, für die sich für eine bestimmte Zahl n>2 immer sagen lässt:
(p^2) | n^q
Hier ein Lösungsansatz von mir:
Würde man (die bisher noch unbewiesene) These zu Rate ziehen, dass zwischen zwei Quadraten immer mindestens eine Primzahl liegt, dann wäre das Doppelte des Quadrates einer Primzashl immer größer als das Quadrat der nächsthöheren Primzahl, und, es wäre, wandert man den Zahlenstrang entlang, zwischen diesen Quadraten nicht immer genug Platz für (p-1) neue Primzahlen geben, so, dass es wenigstens eine Zahl n gäbe, für die es unendlich viele Exponenten p gibt, allerdings müsste der Beweis noch präzisiert werden.
* Diese Frage soll allerdings kurz vor der Lösung stehen.
****************************
****************************
****************************
3) Die ersten Ansätze einer Methode zur Beweisführung und deren Kritik
Dieser Fakt lies mich dazu inspirieren, eine Methode zu entwerfen, mittels der sich beweisen liesse, dass eine Wieferich- Primzahl niemals eine Mirimanoff-Primzahl sein kann; ich möchte dies mal am Fall (p=11) demonstrieren, und gehe dabei davon aus, dass die 11 sowohl Wieferich als auch Mirimanoff - Primzahll sei:
(p^2) | (121-1)^q - 1
Somit lässt sich sagen, dass gilt:
(p^2) | (60*2)^q - 1
Zu dieser Zahl addieren wir den zu (p^2) teilbaren Wert
60*(1 - 2^q)
und erhalten:
(p^2) | 60^q - 1
Wir nehmen also den Wert ((p^2)-1) und teilen ihn durch die Vielfachen von 2 und 3, so, dass wir neue Zahlen n erhalten, für die gilt:
(p^2) | n^q - 1
Alle so erhaltenen Zahlen n schreiben wir in eine Menge M, wobei wir auch sämtliche Vielfachen dieser Zahlen n, die kleiner als (p^2) sind, in die Menge schreiben können, denn, wenn gilt:
(p^2) | j^q - 1
und auch gilt:
(p^2) | k^q -1
, dann gilt auch:
(p^2) | (j*k)^q - 1
Somit können wir also alle ganzzahligen Vielfachen aller Zahlen n in die Menge M schreiben, als auch alle ganzzahligen Brüche, deren Teiler Elemente von M sind, sowie sämtlichr Differenzen des Wertes (121-n) mit n € M.
Das wären dann also die Werte 60, 30, 15, und, da 15 durch 3 teilbar ist, auch die 5.
Weiterhin stünden in dieser Menge dann die
(121 - 16) = 105, die 35 = 105/3 und die 7 = 35/5
Wenn in de Menge M dann alle zu p teilerfremden Primzahlen stehen, dan gibt es unter (p^2) mehr als (p-1) Zahlen n, für die gilt:
(p^2) | n^q - 1
Allerdings liesse sich diese Methode auch auf die Zahlen n anwenden, wenn nicht beide Zahlen 2 und 3 Elemente dieser Menge sind; ausgehend also von den (p-1) Zahlen "n" für eine Primzahl müssten sich somit mehr als (p-1) Zahlen generieren lassen, was aber natürlich nicht möglich sein kann, so, dass diese Methode zumindest in einigen Fällen nur eine begrenzte Anzahl von Zahlen n (und zwar höchstens (p-1) Zahlen) generieren kann.
Dabei hat man großen Spielraum, denn, da ja auch der Wert
(d*p + n)^q - (n^q) durch (p^2) teilbar ist, könnte man auch die Zahl
(d*p + n) in die Menge M schreiben sowie deren Teiler, die sich bei der Teilung durch die Vielfachen der Elemente der Menge M ergeben, sowie sämtliche positiven Zahlen, die danach beim Abzug der Vielfachen von (p^2)von den Zahlen n entstehen.
Zwar hat diese Methode, setzt man n=2 bzw. n=3 ein, den Vorteil, dass man zu Anfang recht viele Zahlen erhällt, da immer gilt:
2*2*2*3 | ((p^2)-1)^q - 1 = (p+1)*(p-1)
, aber, ein Garant für den Erfolg dieser Methode ist dies nicht; ein einziges Gegenbeispiel würde sämtliche Hoffnungen begraben, und, die Wahrscheinlichkeit, mit zunehmender Höhe der Primzahl weniger Zahlen zu erhalten, würde sich erhöhen; hier mal im nächsten Kapitel eine Begründung des Verdachtes dafür, warum das Ganze so ist.
****************************
****************************
****************************
4) Kritik dieser Methode
Nun wollte ich aber testen, ob diese Methode auch für Primzahlen statt für deren Quadrate gilt, das heisst, man beginnt, die Zahl (p-1) durch 2 bzw. 3 zu teilen bzw. mit dem Wert (p-2) oder aber (p-3) zu beginnen.
Ein Beispiel für (p = 23):
23 - 3 = 2*2*5
23 - 2*2*2 = 7
(23 - 1)/2 = 11
23 - 2*5 = 13
23 - 2*3 = 17
23 - 2*2 = 19
Man erhällt also sämtliche Primzahlen (2, 3, 5, 7, 11, 13, 17 und 19), die kleiner als 23 sind, und, somit auch sämtliche Vielfache dieser Zahlen, also, genau (p-1) Zahlen n mit n
Dies hat für alle Primzahlen bis p = 73 funktioniert, aber, hier kommt man (z.B.) nie auf den Wert n=5, auch dann nicht, wenn man den Wert
(d*73 + n)^q - (n^q)
einsetzt und die ganzzahligen Teiler von
(d*73 + n)
mit den teilenden Zahlen, die in M zu finden sind, bildet.
Werden die Primzahlen noch größer, häufen sich die Ausnahmen, weswegen meine Vermutung steht, dass dies auch für die Quadrate der Primzahlen Gültigkeit hat.
****************************
****************************
****************************
5) Noch ein Beweisindikator
Es sei außerdem noch erwähnt, dass sich die Vermutung, dass niemals gleichzeitig gelten kann:
(p^2) | 2^q - 1 sowie (p^2) | 3^q - 1
sich beweisen liesse, wenn sich beweisen lässt, dass sich für jede Primzahl p die Variablen s und t finden lassen, für die gilt:
p || 2^s - 3^t
Die Beweisführung ist recht einfach:
Angenommen, es sei so, dann würde gelten:
(p^2) | 2^(2*s*p) - 3^(2*t*p) (AUSDRUCK 1)
, seien aber beide Primzahlen sowohl Wieferich als auch Mirimanoff-Primzahlen, dann würde aber auch gelten:
(p^2) | 2^(2*s*q) - 3^(2*t*q) (AUSDRUCK 2)
mit q = (p-1)
und somit, sei m = 1 der ggT zwischen p und q, würde auch gelten:
(p^2) | 2^(2*s*m) - 3^(2*t*m) (AUSDRUCK 3)
, was aber nicht sein kann, da sonst gelten würde:
(p^2)|| 2^s - 3^t
, was aber der Ausgangsannahme widerspricht.
So gilt für p = 23 beispielsweise:
(23^2) | 2^22 - 3^22
aber, es gilt auch:
23 || 3^3 - 2^2 = 27 - 4 = 23
****************************
****************************
****************************
6) Kurzintermezzo:
Erwähnt sei noch, dass die 11 eine Mirimanoff-Primzahl ist und für die 23 gilt:
(23^2) | 3^22 - 2^22
Allerdings gibt es auch einen Ausdruck der Natur:
23 || 2^s - 3^t ___ mit (s = 2) und (t = 3), so, dass sich beweisen lässt, dass die 23 weder Wieferich noch Mirimanoff - Primzahl ist.
Ähnlich lässt sich beweisen, dass die 1093 keine Mirimanoff-Primzahl ist, denn es gilt:
(3^7) - 1 = 2*1093
****************************
****************************
****************************
7) Eine Methode, die nachweislich nicht zwangsweise funktioniert:
Es stellt sich die Frage, ob man vielleicht, kennt man neben 1 und ((p^2)-1) noch eine weiter Zahl n, für die gilt:
(p^2) | n^q - 1
sich nach meinem Algorythmus vielleicht sämtliche (p-1) Zahlen n generieren liessen; für p=11 und n=3 geht dies zum Beispiel; nehmen wir aber mal den Fall:
p=13
Zunächst wird es schwer, überhaupt eine Zahl n zu finden, für die gilt:
(p^2) | n^12 - 1
wenn n größer ist als 1 und kleinere ist als (p^2-1), aber, es gibt einen Trick, dies zu bewerkstelligen:
Wir nehmen eine Zahl n=a, für die das nicht gilt; es gilt somit:
(p^2) | a^q - 1 - b*p (Ausdruck 1)
(mit a
(p^2) | ((x*p)+a)^q - 1 (Ausdruck 2)
Wir multiplizieren also diesen Wert mit ((x*p)+a) und erhalten:
(p^2) | ((x*p)+a)^p - x*p - a (Ausdruck 3)
Davon subtrahieren wir den durch (p^2) teilbaren Wert
((x*p)+a)^p - a^p
und erhalten:
(p^2) | a^p - x*p - a (Ausdruck 4)
Davon subtrahieren wir das a-fache vom Ausdruck 1
(p^2) | a^p - a - a*b*p (Ausdruck 1.1)
(p^2) | a + a*b*p - x*p - a
Somit gilt:
p | a*b - x
Für p = 13 und a = 5 erhalten wir b = 1, und somit gilt:
p | x = 5
und somit:
(p^2) | ((5*13)+5)^q - 1
Was gleichbedeutend ist mit:
(p^2) | 70^12 - 1
Damit lässt sich neben den Zahlen 1 und 168 auch die Zahl 70 und somit auch die Zahl n=90=(p^2)-70 finden.
Doch leider lassen sich so keine anderen Zahlen generieren, denn es gilt:
70^2 = - 1 mod (13^2)
sowie
99^2 = - 1 mod (13^2)
Sämtliche Vielfachen von 70 und 99 sind also entweder um eins kleiner oder aber um eins größer als die Vielfachen von (p^2); so geht es also nicht; mit dieser Methode lassen sich aber mit den ersten (p-1) Zahlen sämtliche Zahlen n mit n < (p^2) generieren, für die gilt:
(p^2) | n^q - 1
****************************
****************************
****************************
8) Erste Ansätze zu einem funktionierenden Beweis:
Angenommen, p sei eine Wieferich - Primzahl, dann kann es mit n<(p^2) keine Zahl
n = (x*p + 2) ____ mit x < p
geben, für die gilt:
(p^2) | (x*p + 2)^q - 1
Somit muss (mit a < p) dann immer gelten:
(p^2) | (x*p + 2)^q - 1 - a*p
Nun rechnen wir weiter:
(p^2) | (x*p + 2)^p - x*p - 2 - a*x*(p^2) - 2*a*p
Davon ziehen wir in zwei Schritten folgende durch (p^2) teilbaren Zahlen ab:
(x*p + 2)^p - 2^p ___ sowie ___ 2^p - 2
Es gilt dann:
(p^2) | 2 - x*p - a*x*(p^2) - 2*a*p
und somit:
p | (x + 2a)
Nun lässt sich dann für jede Zahl p ein Zahlenpaar (x;a) mit den Variablen x und a finden, für die das gilt, wenn in jedem Zahlenpaar die Variable x und a genau einmal vorkommt, sei x bzw. a eine Zahl zwischen 0 und p; ein Beispiel mit (p=7):
(x;a) = (1;3), (2;6), (3;2), (4;5), (5;1) (6;4)
Ist p dann auch nioch Mirimanoff - Primzahl, lassen dich Variablen für y und b finden, für die jeweils gilt:
p | y + 3*b
Auch hierfür gibt es immer Beispiele, so, dass, wenn man bedenkt, dass es immer eines der (p-1) Zahlenpaare gibt, für die x = y ist, und somit gilt:
p | 3*b - 2*a ____ und ___ p | 2*x + 3*b + 2*a
Nachweislich lassen sich für jede Primzahl solche Variablen x,y, a und b finden, so, dass hier auf diese Art keine Beweisführung erfolgen kann.
Hier der Beweis:
Zunächst wird bewiesen, dass, ist p eine ungerade Primzahl, sich für eine konstante n immer zwei Zahlen x und a, die beide kleiner sind als p und größer als 0, finden lassen, so, dass gilt:
p | x + a*n
Wir setzen zuerst für a eine Zahl zwischen 0 und p, und varieren, beginnend mit (x=1) den Wert für x, welcher jeweils um 1 ansteigt, so, dass gilt:
x + a*n = m
Es steigt also m immer um jeweils 1 an, und, noch bevor x die Größe p erreicht oder aber überschritten hat, gilt:
p | x + a*n = m
Somit lässt sich für jedes a ein zugeordneter Wert x finden, aber, es ist noch nicht bewiesen, dass die Werte für x und a in den (p-1) Zahlenpaaren (x;a) nicht doppelt vorkommen, aber, das ist recht schnell bewiesen:
Angenommen, es gilt:
p | (x_1) + n*(a_1) ____ als auch ____ p | (x_2) + n*(a_2)
und, entweder die Werte (x_1) und (x_2) seien gleich, oder aber, die Werte (a_1) und (a_2), dann müsste nämlich auch gelten:
p | (x_1) - (x_2) + n*((a_1) - (a_2))
,womit (x_1) = (x_2) nur dann gelten kann, wenn auch gilt: (a_1) = (a_2), weil n zu p teilerfremd ist, und die Werte für x und a kleiner als p sind.
****************************
****************************
****************************
9) Ein interessanter Beweisansatz
Hier wird ein recht interessanter Beweisansatz vorgestellt, um zu beweisen, dass Wieferich - Primzahlen keine miranimoff - Primzahlen sind. Als Beispiel für die Vorgehensweise dient (p=7), das heißt, es wird so getan, als ob gelten würde:
(p^2) | 2^6 - 1 __ und __ (p^2) | 3^6 - 1
Wäre dies so, könnten folgende Aussagen getroffen werden:
p | 1 + 2 + 3 + 2 + 1 = (n_1)
p | 1 + 2*2 + 3*(2^2) + 2*(2^3) + 1*(2^4) = (n_2)
p | 1 - 2*4 + 3*(4^2) - 2*(4^3) + 1*(4^4) = (n_3)
p | 1 + 2*8 + 3*(8^2) + 2*(8^3) + 1*(8^4) = (n_4)
Die Basen 2;4 und 8 sind für jeden primen Exponenten p gleich, deren Exponenten steigen von (p-3) bis (p-p) in Stufen zu je 1 ab. Die Koefizienten ergeben sich für (p=7) wie folgt:
Die Bebene für das pascalsche Dreieck für die Zahl 7 = p weist folgende Zahlenfolge für (p-1) auf:
1; 6; 15; 20; 15; 6; 1 auf.
Wir addieren dazu
- 1 + 1 - 1 + 1 - 1 + 1 - 1
und teilen die entstehende Zahlenfolge dann durch p (=7):
1; 2; 3; 2; 1
Und so werden diese Ausdrücke erzeugt:
------ So wird (n_1) erzeugt:
p | 1 + 2 + 3 + 2 + 1 = (n_1)
Zunächst werden die Koeffizienten für (p-1)
gesucht; deren Summe ist immer gleich 2^(p-1), was man erkennt, wenn man die Zahl
(1+1)^(p-1) als Summenfolge darstellt.
Ist p dann also Wieferich-Primzahl, dann wird von diesem Wert
1 + 6 + 15 + 20 + 15 + 6 + 1
die Zahl (-1) als Summenfolge
- 1 + 1 - 1 + 1 - 1 + 1 - 1
abgezogen, der entstehende Wert 2^6 - 1 ist dann durch (p^2) teilbar.
Teilen wir ihn durch p, entsteht der Wert:
p | 1 + 2 + 3 + 2 + 1
, was für p = 7 natürlich nicht gilt, weil die 7 keine Wieferich - Primzahl ist.
------ So wird dr Wert (n_2) erzeugt:
p | 1 + 2*2 + 3*(2^2) + 2*(2^3) + 1*(2^4) = (n_2)
Zunächst gilt:
(p^2) | 3^6 - 1 ___ und somit: ___ (2+1)^6 - 1
Dies wird als Summenfolge dargestellt:
2^6 + 6*(2^5) + 15*(2^4) + 20*(2^3) + 15*(2^2) + 6*2
Davon wird der durch (p^2) teilbare Wert (2^6) - 1 subtrahiert:
(p^2) | 6*(2^5) + 15*(2^4) + 20*(2^3) + 15*(2^2) + 6*2 + 1
Dazu wird der durch (p^2) teilbare Wert ((2^6)-1)/(2+1) als Summenfolge addiert:
(p^2) | 2^5 - 2^4 + 2^3 - 2^2 + 1
Es gilt nun:
(p^2=) | 7*(2^5) + 14*(2^4) + 21*(2^3) + 14*(2^2) + 7*2
Eine Kontrollrechnung macht das deutlich; dieser Wert ist nämlich gleich:
(p^2) | ((2 + 1)^7 - 3) - ((2^7) - 2)
Der entstehende Wert wird durch 7*2 geteilt, und, es gilt nun:
p | 1 + 2*2 + 3*(2^2) + 2*(2^3) + 1*(2^4) = (n_2)
------So wird der Wert (n_3) erzeugt:
p | 1 - 2*4 + 3*(4^2) - 2*(4^3) + 1*(4^4) = (n_3)
Man nimmt den durch (p^2) teilbaren Wert
(p^2) | (4 - 1)^6 - 1
Und stellt diesen als Summenfolge dar:
(p^2) | 4^6 - 6*(4^5) + 15*(4^5) - 20*(4^4) + 15*(4^3) - 6*4
Davon ziht man den durch (p^2) teilbaren Wert ((4^6)-1) ab, und erhällt nun:
(p^2) | - 6*(4^5) + 15*(4^5) - 20*(4^4) + 15*(4^3) - 6*4 + 1
Dazu addiert man den durch (p^2) teilbaren Wert
(p^2) | - 4^5 - 4^4 - 4^3 - 4^2 - 4 - 1 = ((4^6)-1)/(4-1)
Es ergibt sich nun:
(p^2) | - 7*(4^5) + 14*(4^4) - 21*(4^3) + 14*(4^2) - 7*4
Dieser Wert wir durch (-1)*(p = 7)*4 geteilt, und, es ergibt sich:
(p^2) | + (4^4) - 2*(4^3) + 3*(4^2) - 2*4 + 1
Eine Kontrollrechnung könnte derart lauten:
(p^2) | (4^6) - 4*(3^6) + 3
Dann gilt auch:
(p^2) | ((4^6) - 4*(3^6))^6 - 3^6
Von diesem Wert werden die durch (p^2) teilbaren Werte
(4^(6*6)) - 1 und (4^6)*(3^(6*6)) und 1 - (3^6) subtrahiert.
Die sich ergebende Summenfolge enthällt immer die Werte
k*(2^6*(6-d))*(3^(6*d))
Von dieser werden dann die durch (p^2) teilbaren Werte
k*(3^(6*d))*((2^6)*(6-d) - 1) ____ sowie k*((3^(6*d) -1)
subtrahiert, der Rest erfolgt wie gehabt.
So wird der Wert (n_3) erzeugt:
p | 1 + 2*8 + 3*(8^2) + 2*(8^3) + 1*(8^4) = (n_4)
Man nimmt den Wert
(p^2) | (8+1)^6 - 1
und stellt ihn als Summenfolge dar.
Dazu wird der Wert
(p^2) | 1 - (8^6) addiert sowie die Summenfolge
(p^2) | 8^5 - 8^4 + 8^3 - 8^2 - 8 + 1 = ((8^6)-1)(8+1)
addiert, und, der Rest wird durch (p=7) geteilt.
Gibt es nun tatsächlich keine Primzahlen, die gleichzeitig Wieferich als auch Mirimanoff - Primzahlen sind, dann können nicht alle 4 Gleichungen zugleich durch p teilbar sein.
Ähnliche Ausdrücke erhällt man, wenn man die durch (p^2) teilbaren Zahlen
(p^2) | (3-1)^q - 1____ oder ____ (9 - 1)^q - 1
Als Ausgangsbasis nimmt.
Man kann auch Zahlen der Natur
(4 + 1)^q - (2+3)^q - 4^q - 1^q + 2^q + 3^q
oder Ähnliches als Ausgangsbasis nehmen.
Für (p=5) gilt z.B.
((2^q) - 1)/(2-1) = 2^5 + 2^4 + 2^3 + 2^2 + 2 + 1
((2^q) - 1)/(2+1) = 2^5 - 2^4 + 2^3 - 2^2 + 2 - 1
((3^q) - 1)/(3-1) = 3^5 + 3^4 + 3^3 + 3^2 + 3 + 1
((3^q) - 1)/(3+1) = 3^5 - 3^4 + 3^3 - 3^2 + 3 - 1
Und ganz allgemein gilt:
(p^2) | ((2 + 1)^q) - 1
(p^2) | ((3 - 1)^q - 1
(p^2) | (2 + 1)^p - 2^p - 3 + 2
(p^2) | (3 - 1)^p - 3^p - 2 + 1
(p^2) | (8 + 1)^q - 8^q - 1
(p^2) | (9 - 1)^q - 9^q - 2
(p^2) | (4 - 1)^p - 4^p - 3 + 4
(p^2) | (4 - 1)^q - 1 - 4^q + 1
usw.
Ausserdem lassen sich die Zahlen
(9^q - 1)/(9-1)
(9^q - 1)/(9+1)
(8^q - 1)/(8-1)
(8^q - 1)/(8-1)
Als Summenfolgen darstellen.
Es stellt sich abschliessend die Frage, on (n_2), (n_3) oder (n_4) nicht auch durch p teilbar sind, wenn p weder Wieferich oder aber Mirimanoff - Primzahl ist.
Die könnte zwar für einzelne dieser Zahlen gelten, aber, nicht für alle drei Zahlen zu gleich; ich will die mal exemplarisch an einem Beispiel verdeutlichen:
(n_2) = ((2+1)^p - (2^p) - 1)/2*3*p
(n_3) = ((4-1)^p - (4^p) + 1)/4*3*p
Wäre allso z.B. p keine Wieferich-Primzahl, und wären trotzdem beide Zahlen im Zähler durch (p^2) teilbar, dann müsste auch die Differenz beider Zahlen durch (p^2) teilbar sein:
(p^2) | (3^p) - (2^p) - (3^p) + (4^p) - 2
(p^2) | (4^p) - (2^p) - 2
Ist p dann nicht Wieferich - Primzahl, dann gilt:
(p^2) | (2^p) - 2 - a*p
und somit auch:
(p^2) | (2^p)^2 - (2 + a*p)^2
und somit:
(p^2) | (4^p) - 4 - 4*a*p
Nun addieren wir zum Wert
(p^2) | (4^p) - (2^p) - 2
Den Wert:
(p^2) | - (4^p) + 4 + 4*a*p + (2^p) - 2 - a*p
und erhalten:
(p^2) | 3*a*p
Was natürlich mit zu p teilerfremden Zahlen a und 3 nicht geht.
Für die anderen Zahlen wird ein ähnliches Verfahren angewandt; gibt es also keine Primzahl, die gleichermaßen Wieferich als auch Mirimanoff-Primzahl ist, muss wenigstens einer der vier Werte (n_1), (n_2), (n_3) oder (n_4) nicht die Eigenschaft haben, durch p teilbar zu sein.
****************************
****************************
****************************
10) Ein mißlungener Beweisansatz:
Hier also nun zum Abschluss zur misslungenen Beweisführung, dass Wieferich-Primzahlen niemals Mirimanoff-Primzahlen sein können:
Die Zahlendefinition:
q = (p-1)
d = (p-2)
x < p
a < p
Im Vorlauf wird zunächst bewiesen, dass, wenn gilt:
(p^2) | ((x*p + 2)^q) - 1 - a*p
auch gelten muss:
p | (x + 2*a)
Vorlauf:
Nun zur Beweisführung:
(p^2) | ((x*p + 2)^q) - 1 - a*p (AUSDRUCK 1)
Dies ist gleichbedeutend mit:
(p^2) | ((x*p + 2)^q) - 4 + 3 - a*p (AUSDRUCK 2)
Damit gilt auch:
(p^2) | (((x*p + 2)^q) - 4)^q - (3 - a*p)^q (AUSDRUCK 3)
,da dieser Wert immer durch die Differenz der Basen teilbar ist.
Das Ganze wird mit (((x*p + 2)^q) - 4) multipliziert
(p^2) | (((x*p + 2)^q) - 4)^p - ((3 - a*p)^q)*(((x*p + 2)^q) - 4)
(AUSDRUCK 4)
Da nun nach den kleinen fermatschen Satz gilt:
p | (((x*p + 2)^q) - 4) - (1 - 4)
Gilt nach der "Teilbarkeitsregel T" dann:
(p^2) | (((x*p + 2)^q) - 4)^p - (1 - 4)^p
Dieser Wert wird dann vom Ausdruck 4 abgezogen, und es gilt:
(p^2) | - (3^p) - ((3 - a*p)^q)*(((x*p + 2)^q) - 4)
(AUSDRUCK 5)
Dazu wird die durch (p^2) teilbare Zahl ((3^p) - 3) addiert:
(p^2) | - 3 - ((3 - a*p)^q)*(((x*p + 2)^q) - 4)
(AUSDRUCK 6)
Dies ist gleich:
(p^2) | - 3 - (((3 - a*p)*(x*p + 2))^q) + 4*(3 - a*p)^q
(AUSDRUCK 7)
Dies ist gleich:
(p^2) | - 3 - (3*x*p - x*a*(p^2) - 2*a*p + 6)^q - 4*(3 - a*p)^q
(AUSDRUCK 7)
Dazu wird der durch (p^2), weil immer durch die Differrenz der Basen teilbare Wert
(3*x*p - x*a*(p^2) - 2*a*p + 6)^q - (3*x*p - 2*a*p + 6)^q
addiert, und es ergibt sich:
(p^2) | - 3 - (3*x*p - 2*a*p + 6)^q + 4*(3 - a*p)^q
(AUSDRUCK 7)
Da nun gilt: p | (x + 2*a)
Ist der Wert
(3*x*p - 2*a*p + 6)^q - (6 - 6*a - 2*a)^q
auch immer durch p teilbar, weil er durch die Differenz der Basen teilbar ist.
Dieser Wert wird z,m Ausdruck 7 addiert:
(p^2) | - 3 - (6 - 8*a*p)^q + 4*(3 - a*p)^q
(AUSDRUCK 8)
Nun wird eine k-Darstellung der beiden Zahlen, die mit q potenziert wurden, gemacht, und alle Zahlen, die durch (p^2) teilbar sind, entfernt:
(p^2) | - 3 - 6^q + q*(6^d)*8*a*p + 4*(3^q) - 4*q*(3^d)*a*p
(AUSDRUCK 9)
Zu diesem Ausdruck werden die durch (p^2) teilbaren Werte
(6^q) - 1 sowie 4*(1 - (3^q) addiert; es ergibt sich:
(p^2) | q*(6^d)*8*a*p - 4*q*(3^d)*a*p
(AUSDRUCK 10)
Dieser Ausdruck wird durchg das zu p teilerfremde q geteilt und mit 6 multipliziert.
Dazu werden dann die durch (p^3) teilbaren Werte
(1 - (6^q))*8*a*p und ((3^q)-1)*2*4*a*p
addiert; der entstehende Wert
8*a*p - 8*a*p
ist gleich Null.
So geht es also nicht!
Vom Prinzip her scheitert diese Methode an derselben Sache, wie die Versuche, den Fall 1 der fermatschen Vermutung auf die von mir beschriebene Art und Weise beweisen zu wollen:
Man zieht die Vielfachen dessen, von dem man ausgegengen ist, von dem Ausgangswert derart ab,m dass man am Ende dasselbe, was man vorher addiert hat, hinterher wieder subtrahiert.
****************************
****************************
****************************
11) Der Rest vom Schützenfest:
Es sei noch erwähnt, dass, sei p eine Wieferich - Primzahl, und, wenn gilt:
p | x - y
Dann auch immer gilt:
(p^2) | (x + y)^p - x^p - y^p
Zunächst wird der Wert (x+y)^p als Summenfolge mittels den Koeffizienten des pascalschen Dreieckes dargestellt. Von diesem Wert werden dann die beiden Summanden (x^p) und (y^p) abgezogen. Die restlichen Summanden haben dann immer die Form:
k*(x^d)*(y^(p-d))
Von diesem Wert wird dann folgend Zahl, die durch (p^2) teilbar sind, abgezogen:
1: Schritt: k*(x^d)*((y^(p-d) - (x^(p-d)))
(Die Koeffizienten "k" sind immer durch p teilbar; ein Beispiel für (p=7):
(1) + 7 + 21 + 35 + 35 + 21 + 7 + (1)
Es entsteht der Summand:
k*(x^p)
Die Summe aller Summanden ist dann:
(k_1)*(x^p) + (k_2)*(x^p) + ..... (k_(p-1))*(x1p) + (k_p)*(x^p)
welche gleich dem Wert
(x^p)*((k_1) + (k_2) + ...... (k_(p-1)) + (k_p)
ist; die Summe aller Koeffizienten ist dann aber immer gleich ((2^p)-2); hier mal ein Beispiel für (p=7):
7 + 21 + 35 + 35 + 21 + 7 = 126 = (128 - 2) = (2^7) - 2
****************************
****************************
****************************
Ende: MO 21. Februar 2011
****************************
Kapitelübersicht:
1) Was sind Wieferich und Mirimanoff Primzahlen?
2) Wieviele dieser Primzahlen gibt es?
3) Die ersten Ansätze einer Methode zur Beweisführung und deren Kritik
4) Kritik dieser Methode
5) Noch ein Beweisindikator
6) Kurzintermezzo
7) Eine Methode, die nachweislich nicht funktioniert
8) Erste Ansätze zu einem funktionierenden Beweis
9) Ein interessanter Beweisansatz
10) Ein mißlungener Beweisansatz
11) Der Rest vom Schützenfest
****************************
****************************
****************************
1) Was sind Wieferich und Mirimanoff Primzahlen?
Im Jahre 1909 konnte der Mathematiker Arthur Wieferich für den Fall 1 der fermatschen Vermutung beweisen, dass der Exponent p (die fermatsche Vermutung braucht nur für ungerade prime Exponenten bewiesen zu werden) eine Wieferich-Primzahl sein muss, das heisst, dass gilt:
(p^2) | (2^(p-1)) - 1
Es gibt nur zwei bekannte Wieferich Primzahlen, nämlich die 3511 und die 1093. Sollte es noch mehr geben, müssen sie sehr groß sein, siehe den Link links auf dieser Seite, der hier noch einmal wiederholt wird:
http://books.google.de/books?id=-nEM9ZVr4CsC&pg=PA237&lpg=PA237&dq=Mirimanoff+Primzahl&source=bl&ots=pGk-zUiTBa&sig=UPWvBoRW9I3Wv2CbXosdPORun5A&hl=de&ei=rflGTa68CMWOswag9bGzDg&sa=X&oi=book_result&ct=result&resnum=9&ved=0CDUQ6AEwCA#v=onepage&q=Mirimanoff%20Primzahl&f=false
Im Jahre 1910 konnte dann Dimitry Mirimanoff beweisen, dass für den Fall 1 der fermatschen Vermutung auch gelten muss:
(p^2) | (3^(p-1)) - 1
Die Primzahl 11 ist z.B. eine solche "Mirimanoff - Primzahl" (eine eigene Wortkreation von mir). Die beiden bekannten Wieferich - Primzahlen sind übrigends keine Mirimanoff - Primzahlen.
Wer nun beweisen kann, dass eine Wieferich-Primuzahl niemals Mirimanoff-Primzahl sein kann, hätte also den Fall 1 der fermatschen Vermutung bewiesen, ebenso wie jene These, dass es nur zwei Wieferich - Primzahlen (die 1093 und die 3511) gibt, denn für jede einzelne Primzahl als Exponent kann die fermatsche Vermutung mit speziellen Methoden bewiesen werden.
****************************
****************************
****************************
2) Wieviele dieser Primzahlen gibt es?
Es lässt sich auch beweisen, dass es zwischen 0 und (p^2) immer genau (p-1) Zahlen n gibt, für die gilt:
(p^2) | n^(p-1) - 1
Dies geht so:
Man definiert (p-1) Gruppen, mit je p Zahlen x, die nicht durch p teilbar sind mit jeweils x<(p^2), für die gilt, dass innerhalb einer Gruppe, seien zwei Zahlen j und k konkrete Zahlen der Variable x, immer gilt:
p | j-k .
Damit gilt aufgrund des kleinen fermatschen Satzes mit q=(p-1):
p | j^q - k^q
Würde aber nun gelten:
(p^2) | j^q - k^q
, dann könnte man diesen Wert mit k multiplizieren und die durch (p^2) teilbare Zahl
(k^p) - (j^p)
addieren; es würde somit gelten:
(p^2) | (j^q)*(k - j)
, was aber nicht sein kann, da j zu p teilerfremd ist, und es gilt:
p || (k-j)
Somit lässt sich für jede Zahl x aus einer der p Zahlen umfassenden Gruppe sagen:
(p^2) | x^q - 1 - a*p
Mit a < p und einem für jede Zahl x innerhalb einer Gruppe jeweils anderen Wert für a, so dass in jeder der (p-1) Gruppen der Wert (a=0) genau einmal vorkommt, und, somit gilt für genau (p-1) Zahlen x mit x>(p^2) gilt:
(p^2) | x^(p-1) - 1
Bei p = 5 lauten diese 4 (bzw. (p-1)) Zahlen z.B.
1, 7, 18, 24
, für p = 11 lauten sie:
1, 3, 9, 27, 40, 81, 94, 112, 118, 120
Logischerweise sind die Zahlen 1 und ((p^2)-1) immer vorhanden, und auch ansonsten ist eine Symmetrie da; immer, wenn gilt:
(p^2) | n^q - 1
, auch gelten muss:
(p^2) | ((p^2) - n)^q - (n^q)
, da letzterer Wert immer durch die Summe der Basen teilbar ist, und somit gilt auch:
(p^2) | ((p^2) - n)^q - 1
Es stellt sich die (ungeklärte) Frage*, ob es unendliche viele Primzahlen p gibt, für die sich für eine bestimmte Zahl n>2 immer sagen lässt:
(p^2) | n^q
Hier ein Lösungsansatz von mir:
Würde man (die bisher noch unbewiesene) These zu Rate ziehen, dass zwischen zwei Quadraten immer mindestens eine Primzahl liegt, dann wäre das Doppelte des Quadrates einer Primzashl immer größer als das Quadrat der nächsthöheren Primzahl, und, es wäre, wandert man den Zahlenstrang entlang, zwischen diesen Quadraten nicht immer genug Platz für (p-1) neue Primzahlen geben, so, dass es wenigstens eine Zahl n gäbe, für die es unendlich viele Exponenten p gibt, allerdings müsste der Beweis noch präzisiert werden.
* Diese Frage soll allerdings kurz vor der Lösung stehen.
****************************
****************************
****************************
3) Die ersten Ansätze einer Methode zur Beweisführung und deren Kritik
Dieser Fakt lies mich dazu inspirieren, eine Methode zu entwerfen, mittels der sich beweisen liesse, dass eine Wieferich- Primzahl niemals eine Mirimanoff-Primzahl sein kann; ich möchte dies mal am Fall (p=11) demonstrieren, und gehe dabei davon aus, dass die 11 sowohl Wieferich als auch Mirimanoff - Primzahll sei:
(p^2) | (121-1)^q - 1
Somit lässt sich sagen, dass gilt:
(p^2) | (60*2)^q - 1
Zu dieser Zahl addieren wir den zu (p^2) teilbaren Wert
60*(1 - 2^q)
und erhalten:
(p^2) | 60^q - 1
Wir nehmen also den Wert ((p^2)-1) und teilen ihn durch die Vielfachen von 2 und 3, so, dass wir neue Zahlen n erhalten, für die gilt:
(p^2) | n^q - 1
Alle so erhaltenen Zahlen n schreiben wir in eine Menge M, wobei wir auch sämtliche Vielfachen dieser Zahlen n, die kleiner als (p^2) sind, in die Menge schreiben können, denn, wenn gilt:
(p^2) | j^q - 1
und auch gilt:
(p^2) | k^q -1
, dann gilt auch:
(p^2) | (j*k)^q - 1
Somit können wir also alle ganzzahligen Vielfachen aller Zahlen n in die Menge M schreiben, als auch alle ganzzahligen Brüche, deren Teiler Elemente von M sind, sowie sämtlichr Differenzen des Wertes (121-n) mit n € M.
Das wären dann also die Werte 60, 30, 15, und, da 15 durch 3 teilbar ist, auch die 5.
Weiterhin stünden in dieser Menge dann die
(121 - 16) = 105, die 35 = 105/3 und die 7 = 35/5
Wenn in de Menge M dann alle zu p teilerfremden Primzahlen stehen, dan gibt es unter (p^2) mehr als (p-1) Zahlen n, für die gilt:
(p^2) | n^q - 1
Allerdings liesse sich diese Methode auch auf die Zahlen n anwenden, wenn nicht beide Zahlen 2 und 3 Elemente dieser Menge sind; ausgehend also von den (p-1) Zahlen "n" für eine Primzahl müssten sich somit mehr als (p-1) Zahlen generieren lassen, was aber natürlich nicht möglich sein kann, so, dass diese Methode zumindest in einigen Fällen nur eine begrenzte Anzahl von Zahlen n (und zwar höchstens (p-1) Zahlen) generieren kann.
Dabei hat man großen Spielraum, denn, da ja auch der Wert
(d*p + n)^q - (n^q) durch (p^2) teilbar ist, könnte man auch die Zahl
(d*p + n) in die Menge M schreiben sowie deren Teiler, die sich bei der Teilung durch die Vielfachen der Elemente der Menge M ergeben, sowie sämtliche positiven Zahlen, die danach beim Abzug der Vielfachen von (p^2)von den Zahlen n entstehen.
Zwar hat diese Methode, setzt man n=2 bzw. n=3 ein, den Vorteil, dass man zu Anfang recht viele Zahlen erhällt, da immer gilt:
2*2*2*3 | ((p^2)-1)^q - 1 = (p+1)*(p-1)
, aber, ein Garant für den Erfolg dieser Methode ist dies nicht; ein einziges Gegenbeispiel würde sämtliche Hoffnungen begraben, und, die Wahrscheinlichkeit, mit zunehmender Höhe der Primzahl weniger Zahlen zu erhalten, würde sich erhöhen; hier mal im nächsten Kapitel eine Begründung des Verdachtes dafür, warum das Ganze so ist.
****************************
****************************
****************************
4) Kritik dieser Methode
Nun wollte ich aber testen, ob diese Methode auch für Primzahlen statt für deren Quadrate gilt, das heisst, man beginnt, die Zahl (p-1) durch 2 bzw. 3 zu teilen bzw. mit dem Wert (p-2) oder aber (p-3) zu beginnen.
Ein Beispiel für (p = 23):
23 - 3 = 2*2*5
23 - 2*2*2 = 7
(23 - 1)/2 = 11
23 - 2*5 = 13
23 - 2*3 = 17
23 - 2*2 = 19
Man erhällt also sämtliche Primzahlen (2, 3, 5, 7, 11, 13, 17 und 19), die kleiner als 23 sind, und, somit auch sämtliche Vielfache dieser Zahlen, also, genau (p-1) Zahlen n mit n
Dies hat für alle Primzahlen bis p = 73 funktioniert, aber, hier kommt man (z.B.) nie auf den Wert n=5, auch dann nicht, wenn man den Wert
(d*73 + n)^q - (n^q)
einsetzt und die ganzzahligen Teiler von
(d*73 + n)
mit den teilenden Zahlen, die in M zu finden sind, bildet.
Werden die Primzahlen noch größer, häufen sich die Ausnahmen, weswegen meine Vermutung steht, dass dies auch für die Quadrate der Primzahlen Gültigkeit hat.
****************************
****************************
****************************
5) Noch ein Beweisindikator
Es sei außerdem noch erwähnt, dass sich die Vermutung, dass niemals gleichzeitig gelten kann:
(p^2) | 2^q - 1 sowie (p^2) | 3^q - 1
sich beweisen liesse, wenn sich beweisen lässt, dass sich für jede Primzahl p die Variablen s und t finden lassen, für die gilt:
p || 2^s - 3^t
Die Beweisführung ist recht einfach:
Angenommen, es sei so, dann würde gelten:
(p^2) | 2^(2*s*p) - 3^(2*t*p) (AUSDRUCK 1)
, seien aber beide Primzahlen sowohl Wieferich als auch Mirimanoff-Primzahlen, dann würde aber auch gelten:
(p^2) | 2^(2*s*q) - 3^(2*t*q) (AUSDRUCK 2)
mit q = (p-1)
und somit, sei m = 1 der ggT zwischen p und q, würde auch gelten:
(p^2) | 2^(2*s*m) - 3^(2*t*m) (AUSDRUCK 3)
, was aber nicht sein kann, da sonst gelten würde:
(p^2)|| 2^s - 3^t
, was aber der Ausgangsannahme widerspricht.
So gilt für p = 23 beispielsweise:
(23^2) | 2^22 - 3^22
aber, es gilt auch:
23 || 3^3 - 2^2 = 27 - 4 = 23
****************************
****************************
****************************
6) Kurzintermezzo:
Erwähnt sei noch, dass die 11 eine Mirimanoff-Primzahl ist und für die 23 gilt:
(23^2) | 3^22 - 2^22
Allerdings gibt es auch einen Ausdruck der Natur:
23 || 2^s - 3^t ___ mit (s = 2) und (t = 3), so, dass sich beweisen lässt, dass die 23 weder Wieferich noch Mirimanoff - Primzahl ist.
Ähnlich lässt sich beweisen, dass die 1093 keine Mirimanoff-Primzahl ist, denn es gilt:
(3^7) - 1 = 2*1093
****************************
****************************
****************************
7) Eine Methode, die nachweislich nicht zwangsweise funktioniert:
Es stellt sich die Frage, ob man vielleicht, kennt man neben 1 und ((p^2)-1) noch eine weiter Zahl n, für die gilt:
(p^2) | n^q - 1
sich nach meinem Algorythmus vielleicht sämtliche (p-1) Zahlen n generieren liessen; für p=11 und n=3 geht dies zum Beispiel; nehmen wir aber mal den Fall:
p=13
Zunächst wird es schwer, überhaupt eine Zahl n zu finden, für die gilt:
(p^2) | n^12 - 1
wenn n größer ist als 1 und kleinere ist als (p^2-1), aber, es gibt einen Trick, dies zu bewerkstelligen:
Wir nehmen eine Zahl n=a, für die das nicht gilt; es gilt somit:
(p^2) | a^q - 1 - b*p (Ausdruck 1)
(mit a
(p^2) | ((x*p)+a)^q - 1 (Ausdruck 2)
Wir multiplizieren also diesen Wert mit ((x*p)+a) und erhalten:
(p^2) | ((x*p)+a)^p - x*p - a (Ausdruck 3)
Davon subtrahieren wir den durch (p^2) teilbaren Wert
((x*p)+a)^p - a^p
und erhalten:
(p^2) | a^p - x*p - a (Ausdruck 4)
Davon subtrahieren wir das a-fache vom Ausdruck 1
(p^2) | a^p - a - a*b*p (Ausdruck 1.1)
(p^2) | a + a*b*p - x*p - a
Somit gilt:
p | a*b - x
Für p = 13 und a = 5 erhalten wir b = 1, und somit gilt:
p | x = 5
und somit:
(p^2) | ((5*13)+5)^q - 1
Was gleichbedeutend ist mit:
(p^2) | 70^12 - 1
Damit lässt sich neben den Zahlen 1 und 168 auch die Zahl 70 und somit auch die Zahl n=90=(p^2)-70 finden.
Doch leider lassen sich so keine anderen Zahlen generieren, denn es gilt:
70^2 = - 1 mod (13^2)
sowie
99^2 = - 1 mod (13^2)
Sämtliche Vielfachen von 70 und 99 sind also entweder um eins kleiner oder aber um eins größer als die Vielfachen von (p^2); so geht es also nicht; mit dieser Methode lassen sich aber mit den ersten (p-1) Zahlen sämtliche Zahlen n mit n < (p^2) generieren, für die gilt:
(p^2) | n^q - 1
****************************
****************************
****************************
8) Erste Ansätze zu einem funktionierenden Beweis:
Angenommen, p sei eine Wieferich - Primzahl, dann kann es mit n<(p^2) keine Zahl
n = (x*p + 2) ____ mit x < p
geben, für die gilt:
(p^2) | (x*p + 2)^q - 1
Somit muss (mit a < p) dann immer gelten:
(p^2) | (x*p + 2)^q - 1 - a*p
Nun rechnen wir weiter:
(p^2) | (x*p + 2)^p - x*p - 2 - a*x*(p^2) - 2*a*p
Davon ziehen wir in zwei Schritten folgende durch (p^2) teilbaren Zahlen ab:
(x*p + 2)^p - 2^p ___ sowie ___ 2^p - 2
Es gilt dann:
(p^2) | 2 - x*p - a*x*(p^2) - 2*a*p
und somit:
p | (x + 2a)
Nun lässt sich dann für jede Zahl p ein Zahlenpaar (x;a) mit den Variablen x und a finden, für die das gilt, wenn in jedem Zahlenpaar die Variable x und a genau einmal vorkommt, sei x bzw. a eine Zahl zwischen 0 und p; ein Beispiel mit (p=7):
(x;a) = (1;3), (2;6), (3;2), (4;5), (5;1) (6;4)
Ist p dann auch nioch Mirimanoff - Primzahl, lassen dich Variablen für y und b finden, für die jeweils gilt:
p | y + 3*b
Auch hierfür gibt es immer Beispiele, so, dass, wenn man bedenkt, dass es immer eines der (p-1) Zahlenpaare gibt, für die x = y ist, und somit gilt:
p | 3*b - 2*a ____ und ___ p | 2*x + 3*b + 2*a
Nachweislich lassen sich für jede Primzahl solche Variablen x,y, a und b finden, so, dass hier auf diese Art keine Beweisführung erfolgen kann.
Hier der Beweis:
Zunächst wird bewiesen, dass, ist p eine ungerade Primzahl, sich für eine konstante n immer zwei Zahlen x und a, die beide kleiner sind als p und größer als 0, finden lassen, so, dass gilt:
p | x + a*n
Wir setzen zuerst für a eine Zahl zwischen 0 und p, und varieren, beginnend mit (x=1) den Wert für x, welcher jeweils um 1 ansteigt, so, dass gilt:
x + a*n = m
Es steigt also m immer um jeweils 1 an, und, noch bevor x die Größe p erreicht oder aber überschritten hat, gilt:
p | x + a*n = m
Somit lässt sich für jedes a ein zugeordneter Wert x finden, aber, es ist noch nicht bewiesen, dass die Werte für x und a in den (p-1) Zahlenpaaren (x;a) nicht doppelt vorkommen, aber, das ist recht schnell bewiesen:
Angenommen, es gilt:
p | (x_1) + n*(a_1) ____ als auch ____ p | (x_2) + n*(a_2)
und, entweder die Werte (x_1) und (x_2) seien gleich, oder aber, die Werte (a_1) und (a_2), dann müsste nämlich auch gelten:
p | (x_1) - (x_2) + n*((a_1) - (a_2))
,womit (x_1) = (x_2) nur dann gelten kann, wenn auch gilt: (a_1) = (a_2), weil n zu p teilerfremd ist, und die Werte für x und a kleiner als p sind.
****************************
****************************
****************************
9) Ein interessanter Beweisansatz
Hier wird ein recht interessanter Beweisansatz vorgestellt, um zu beweisen, dass Wieferich - Primzahlen keine miranimoff - Primzahlen sind. Als Beispiel für die Vorgehensweise dient (p=7), das heißt, es wird so getan, als ob gelten würde:
(p^2) | 2^6 - 1 __ und __ (p^2) | 3^6 - 1
Wäre dies so, könnten folgende Aussagen getroffen werden:
p | 1 + 2 + 3 + 2 + 1 = (n_1)
p | 1 + 2*2 + 3*(2^2) + 2*(2^3) + 1*(2^4) = (n_2)
p | 1 - 2*4 + 3*(4^2) - 2*(4^3) + 1*(4^4) = (n_3)
p | 1 + 2*8 + 3*(8^2) + 2*(8^3) + 1*(8^4) = (n_4)
Die Basen 2;4 und 8 sind für jeden primen Exponenten p gleich, deren Exponenten steigen von (p-3) bis (p-p) in Stufen zu je 1 ab. Die Koefizienten ergeben sich für (p=7) wie folgt:
Die Bebene für das pascalsche Dreieck für die Zahl 7 = p weist folgende Zahlenfolge für (p-1) auf:
1; 6; 15; 20; 15; 6; 1 auf.
Wir addieren dazu
- 1 + 1 - 1 + 1 - 1 + 1 - 1
und teilen die entstehende Zahlenfolge dann durch p (=7):
1; 2; 3; 2; 1
Und so werden diese Ausdrücke erzeugt:
------ So wird (n_1) erzeugt:
p | 1 + 2 + 3 + 2 + 1 = (n_1)
Zunächst werden die Koeffizienten für (p-1)
gesucht; deren Summe ist immer gleich 2^(p-1), was man erkennt, wenn man die Zahl
(1+1)^(p-1) als Summenfolge darstellt.
Ist p dann also Wieferich-Primzahl, dann wird von diesem Wert
1 + 6 + 15 + 20 + 15 + 6 + 1
die Zahl (-1) als Summenfolge
- 1 + 1 - 1 + 1 - 1 + 1 - 1
abgezogen, der entstehende Wert 2^6 - 1 ist dann durch (p^2) teilbar.
Teilen wir ihn durch p, entsteht der Wert:
p | 1 + 2 + 3 + 2 + 1
, was für p = 7 natürlich nicht gilt, weil die 7 keine Wieferich - Primzahl ist.
------ So wird dr Wert (n_2) erzeugt:
p | 1 + 2*2 + 3*(2^2) + 2*(2^3) + 1*(2^4) = (n_2)
Zunächst gilt:
(p^2) | 3^6 - 1 ___ und somit: ___ (2+1)^6 - 1
Dies wird als Summenfolge dargestellt:
2^6 + 6*(2^5) + 15*(2^4) + 20*(2^3) + 15*(2^2) + 6*2
Davon wird der durch (p^2) teilbare Wert (2^6) - 1 subtrahiert:
(p^2) | 6*(2^5) + 15*(2^4) + 20*(2^3) + 15*(2^2) + 6*2 + 1
Dazu wird der durch (p^2) teilbare Wert ((2^6)-1)/(2+1) als Summenfolge addiert:
(p^2) | 2^5 - 2^4 + 2^3 - 2^2 + 1
Es gilt nun:
(p^2=) | 7*(2^5) + 14*(2^4) + 21*(2^3) + 14*(2^2) + 7*2
Eine Kontrollrechnung macht das deutlich; dieser Wert ist nämlich gleich:
(p^2) | ((2 + 1)^7 - 3) - ((2^7) - 2)
Der entstehende Wert wird durch 7*2 geteilt, und, es gilt nun:
p | 1 + 2*2 + 3*(2^2) + 2*(2^3) + 1*(2^4) = (n_2)
------So wird der Wert (n_3) erzeugt:
p | 1 - 2*4 + 3*(4^2) - 2*(4^3) + 1*(4^4) = (n_3)
Man nimmt den durch (p^2) teilbaren Wert
(p^2) | (4 - 1)^6 - 1
Und stellt diesen als Summenfolge dar:
(p^2) | 4^6 - 6*(4^5) + 15*(4^5) - 20*(4^4) + 15*(4^3) - 6*4
Davon ziht man den durch (p^2) teilbaren Wert ((4^6)-1) ab, und erhällt nun:
(p^2) | - 6*(4^5) + 15*(4^5) - 20*(4^4) + 15*(4^3) - 6*4 + 1
Dazu addiert man den durch (p^2) teilbaren Wert
(p^2) | - 4^5 - 4^4 - 4^3 - 4^2 - 4 - 1 = ((4^6)-1)/(4-1)
Es ergibt sich nun:
(p^2) | - 7*(4^5) + 14*(4^4) - 21*(4^3) + 14*(4^2) - 7*4
Dieser Wert wir durch (-1)*(p = 7)*4 geteilt, und, es ergibt sich:
(p^2) | + (4^4) - 2*(4^3) + 3*(4^2) - 2*4 + 1
Eine Kontrollrechnung könnte derart lauten:
(p^2) | (4^6) - 4*(3^6) + 3
Dann gilt auch:
(p^2) | ((4^6) - 4*(3^6))^6 - 3^6
Von diesem Wert werden die durch (p^2) teilbaren Werte
(4^(6*6)) - 1 und (4^6)*(3^(6*6)) und 1 - (3^6) subtrahiert.
Die sich ergebende Summenfolge enthällt immer die Werte
k*(2^6*(6-d))*(3^(6*d))
Von dieser werden dann die durch (p^2) teilbaren Werte
k*(3^(6*d))*((2^6)*(6-d) - 1) ____ sowie k*((3^(6*d) -1)
subtrahiert, der Rest erfolgt wie gehabt.
So wird der Wert (n_3) erzeugt:
p | 1 + 2*8 + 3*(8^2) + 2*(8^3) + 1*(8^4) = (n_4)
Man nimmt den Wert
(p^2) | (8+1)^6 - 1
und stellt ihn als Summenfolge dar.
Dazu wird der Wert
(p^2) | 1 - (8^6) addiert sowie die Summenfolge
(p^2) | 8^5 - 8^4 + 8^3 - 8^2 - 8 + 1 = ((8^6)-1)(8+1)
addiert, und, der Rest wird durch (p=7) geteilt.
Gibt es nun tatsächlich keine Primzahlen, die gleichzeitig Wieferich als auch Mirimanoff - Primzahlen sind, dann können nicht alle 4 Gleichungen zugleich durch p teilbar sein.
Ähnliche Ausdrücke erhällt man, wenn man die durch (p^2) teilbaren Zahlen
(p^2) | (3-1)^q - 1____ oder ____ (9 - 1)^q - 1
Als Ausgangsbasis nimmt.
Man kann auch Zahlen der Natur
(4 + 1)^q - (2+3)^q - 4^q - 1^q + 2^q + 3^q
oder Ähnliches als Ausgangsbasis nehmen.
Für (p=5) gilt z.B.
((2^q) - 1)/(2-1) = 2^5 + 2^4 + 2^3 + 2^2 + 2 + 1
((2^q) - 1)/(2+1) = 2^5 - 2^4 + 2^3 - 2^2 + 2 - 1
((3^q) - 1)/(3-1) = 3^5 + 3^4 + 3^3 + 3^2 + 3 + 1
((3^q) - 1)/(3+1) = 3^5 - 3^4 + 3^3 - 3^2 + 3 - 1
Und ganz allgemein gilt:
(p^2) | ((2 + 1)^q) - 1
(p^2) | ((3 - 1)^q - 1
(p^2) | (2 + 1)^p - 2^p - 3 + 2
(p^2) | (3 - 1)^p - 3^p - 2 + 1
(p^2) | (8 + 1)^q - 8^q - 1
(p^2) | (9 - 1)^q - 9^q - 2
(p^2) | (4 - 1)^p - 4^p - 3 + 4
(p^2) | (4 - 1)^q - 1 - 4^q + 1
usw.
Ausserdem lassen sich die Zahlen
(9^q - 1)/(9-1)
(9^q - 1)/(9+1)
(8^q - 1)/(8-1)
(8^q - 1)/(8-1)
Als Summenfolgen darstellen.
Es stellt sich abschliessend die Frage, on (n_2), (n_3) oder (n_4) nicht auch durch p teilbar sind, wenn p weder Wieferich oder aber Mirimanoff - Primzahl ist.
Die könnte zwar für einzelne dieser Zahlen gelten, aber, nicht für alle drei Zahlen zu gleich; ich will die mal exemplarisch an einem Beispiel verdeutlichen:
(n_2) = ((2+1)^p - (2^p) - 1)/2*3*p
(n_3) = ((4-1)^p - (4^p) + 1)/4*3*p
Wäre allso z.B. p keine Wieferich-Primzahl, und wären trotzdem beide Zahlen im Zähler durch (p^2) teilbar, dann müsste auch die Differenz beider Zahlen durch (p^2) teilbar sein:
(p^2) | (3^p) - (2^p) - (3^p) + (4^p) - 2
(p^2) | (4^p) - (2^p) - 2
Ist p dann nicht Wieferich - Primzahl, dann gilt:
(p^2) | (2^p) - 2 - a*p
und somit auch:
(p^2) | (2^p)^2 - (2 + a*p)^2
und somit:
(p^2) | (4^p) - 4 - 4*a*p
Nun addieren wir zum Wert
(p^2) | (4^p) - (2^p) - 2
Den Wert:
(p^2) | - (4^p) + 4 + 4*a*p + (2^p) - 2 - a*p
und erhalten:
(p^2) | 3*a*p
Was natürlich mit zu p teilerfremden Zahlen a und 3 nicht geht.
Für die anderen Zahlen wird ein ähnliches Verfahren angewandt; gibt es also keine Primzahl, die gleichermaßen Wieferich als auch Mirimanoff-Primzahl ist, muss wenigstens einer der vier Werte (n_1), (n_2), (n_3) oder (n_4) nicht die Eigenschaft haben, durch p teilbar zu sein.
****************************
****************************
****************************
10) Ein mißlungener Beweisansatz:
Hier also nun zum Abschluss zur misslungenen Beweisführung, dass Wieferich-Primzahlen niemals Mirimanoff-Primzahlen sein können:
Die Zahlendefinition:
q = (p-1)
d = (p-2)
x < p
a < p
Im Vorlauf wird zunächst bewiesen, dass, wenn gilt:
(p^2) | ((x*p + 2)^q) - 1 - a*p
auch gelten muss:
p | (x + 2*a)
Vorlauf:
Nun zur Beweisführung:
(p^2) | ((x*p + 2)^q) - 1 - a*p (AUSDRUCK 1)
Dies ist gleichbedeutend mit:
(p^2) | ((x*p + 2)^q) - 4 + 3 - a*p (AUSDRUCK 2)
Damit gilt auch:
(p^2) | (((x*p + 2)^q) - 4)^q - (3 - a*p)^q (AUSDRUCK 3)
,da dieser Wert immer durch die Differenz der Basen teilbar ist.
Das Ganze wird mit (((x*p + 2)^q) - 4) multipliziert
(p^2) | (((x*p + 2)^q) - 4)^p - ((3 - a*p)^q)*(((x*p + 2)^q) - 4)
(AUSDRUCK 4)
Da nun nach den kleinen fermatschen Satz gilt:
p | (((x*p + 2)^q) - 4) - (1 - 4)
Gilt nach der "Teilbarkeitsregel T" dann:
(p^2) | (((x*p + 2)^q) - 4)^p - (1 - 4)^p
Dieser Wert wird dann vom Ausdruck 4 abgezogen, und es gilt:
(p^2) | - (3^p) - ((3 - a*p)^q)*(((x*p + 2)^q) - 4)
(AUSDRUCK 5)
Dazu wird die durch (p^2) teilbare Zahl ((3^p) - 3) addiert:
(p^2) | - 3 - ((3 - a*p)^q)*(((x*p + 2)^q) - 4)
(AUSDRUCK 6)
Dies ist gleich:
(p^2) | - 3 - (((3 - a*p)*(x*p + 2))^q) + 4*(3 - a*p)^q
(AUSDRUCK 7)
Dies ist gleich:
(p^2) | - 3 - (3*x*p - x*a*(p^2) - 2*a*p + 6)^q - 4*(3 - a*p)^q
(AUSDRUCK 7)
Dazu wird der durch (p^2), weil immer durch die Differrenz der Basen teilbare Wert
(3*x*p - x*a*(p^2) - 2*a*p + 6)^q - (3*x*p - 2*a*p + 6)^q
addiert, und es ergibt sich:
(p^2) | - 3 - (3*x*p - 2*a*p + 6)^q + 4*(3 - a*p)^q
(AUSDRUCK 7)
Da nun gilt: p | (x + 2*a)
Ist der Wert
(3*x*p - 2*a*p + 6)^q - (6 - 6*a - 2*a)^q
auch immer durch p teilbar, weil er durch die Differenz der Basen teilbar ist.
Dieser Wert wird z,m Ausdruck 7 addiert:
(p^2) | - 3 - (6 - 8*a*p)^q + 4*(3 - a*p)^q
(AUSDRUCK 8)
Nun wird eine k-Darstellung der beiden Zahlen, die mit q potenziert wurden, gemacht, und alle Zahlen, die durch (p^2) teilbar sind, entfernt:
(p^2) | - 3 - 6^q + q*(6^d)*8*a*p + 4*(3^q) - 4*q*(3^d)*a*p
(AUSDRUCK 9)
Zu diesem Ausdruck werden die durch (p^2) teilbaren Werte
(6^q) - 1 sowie 4*(1 - (3^q) addiert; es ergibt sich:
(p^2) | q*(6^d)*8*a*p - 4*q*(3^d)*a*p
(AUSDRUCK 10)
Dieser Ausdruck wird durchg das zu p teilerfremde q geteilt und mit 6 multipliziert.
Dazu werden dann die durch (p^3) teilbaren Werte
(1 - (6^q))*8*a*p und ((3^q)-1)*2*4*a*p
addiert; der entstehende Wert
8*a*p - 8*a*p
ist gleich Null.
So geht es also nicht!
Vom Prinzip her scheitert diese Methode an derselben Sache, wie die Versuche, den Fall 1 der fermatschen Vermutung auf die von mir beschriebene Art und Weise beweisen zu wollen:
Man zieht die Vielfachen dessen, von dem man ausgegengen ist, von dem Ausgangswert derart ab,m dass man am Ende dasselbe, was man vorher addiert hat, hinterher wieder subtrahiert.
****************************
****************************
****************************
11) Der Rest vom Schützenfest:
Es sei noch erwähnt, dass, sei p eine Wieferich - Primzahl, und, wenn gilt:
p | x - y
Dann auch immer gilt:
(p^2) | (x + y)^p - x^p - y^p
Zunächst wird der Wert (x+y)^p als Summenfolge mittels den Koeffizienten des pascalschen Dreieckes dargestellt. Von diesem Wert werden dann die beiden Summanden (x^p) und (y^p) abgezogen. Die restlichen Summanden haben dann immer die Form:
k*(x^d)*(y^(p-d))
Von diesem Wert wird dann folgend Zahl, die durch (p^2) teilbar sind, abgezogen:
1: Schritt: k*(x^d)*((y^(p-d) - (x^(p-d)))
(Die Koeffizienten "k" sind immer durch p teilbar; ein Beispiel für (p=7):
(1) + 7 + 21 + 35 + 35 + 21 + 7 + (1)
Es entsteht der Summand:
k*(x^p)
Die Summe aller Summanden ist dann:
(k_1)*(x^p) + (k_2)*(x^p) + ..... (k_(p-1))*(x1p) + (k_p)*(x^p)
welche gleich dem Wert
(x^p)*((k_1) + (k_2) + ...... (k_(p-1)) + (k_p)
ist; die Summe aller Koeffizienten ist dann aber immer gleich ((2^p)-2); hier mal ein Beispiel für (p=7):
7 + 21 + 35 + 35 + 21 + 7 = 126 = (128 - 2) = (2^7) - 2
****************************
****************************
****************************
Ende: MO 21. Februar 2011
Abonnieren
Posts (Atom)